Assignment 6 Information

whuang@cs.rpi.edu; email

Problem 3: Chi-squared pruning

 The purpose of chi-squared pruning is to test whether splitting on an attribute contributes a statistically significant amount of information. This is covered in our text on pages 542--3, but you may find the following explanation clearer.

NOTE: The converter I used to create images from the mathematical equations and symbols wasn't working exactly right; that's why you see the horizontal and vertical bars below.

NOTE: In the following discussion, the two classifications "positive" and "negative" are used. For Problem 3 you may assume that there are just two classifications, but you should NOT make any assumptions as to exactly what they are (e.g. yes, no, positive, negative, edible, poisonous, etc.) It's probably not that much more difficult to write your code so that it works with an arbitrary number of classifications.

The chi-squared test is a measurement of whether splitting on a given attribute matters. Before splitting on an attribute, we can characterize how many examples there are for each classification and see how closely each split follows these proportions. If the attribute doesn't matter, then we'd expect that each "split" of training data (as divided by this attribute) to have approximately the same fraction of examples in each classification as the training data did before splitting on this attribute

Suppose the current call to the learn-dtree is given a set of training data $S$. These data have mixed classifications; the number of positive examples in $S$ is $p$, and the number of negative examples is $n$. We know that $p + n = \vert S\vert$.

Through the information analysis, we have picked an attribute that splits $S$ into a number of subsets $S_i$. Each of these subsets will (in general) have mixed classifications. Let $p_i$ be the number of positive examples in $S_i$ and $n_i$ be the number of negative examples. We know that $p_i + n_i = \vert S_i\vert$.

If this attribute was irrelevant, then we would expect that the number of positive examples in $S_i$ would be:

\begin{displaymath} \hat p_i = \frac{p}{p+n} \vert S_i\vert \end{displaymath}

Likewise, we would expect the number of negative examples to be:

\begin{displaymath} \hat n_i = \frac{n}{p+n} \vert S_i\vert \end{displaymath}

Now, we calculate how much ``error'' there is between the actual number of positive and negative examples in each $S_i$ and the expected number.

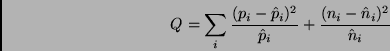
\begin{displaymath} Q = \sum_i \frac{(p_i - \hat p_i)^2}{\hat p_i} + \frac{(n_i - \hat n_i)^2}{\hat n_i} \end{displaymath}

Note that this sum is over each subset created by the split on this attribute. If there are three values for this attribute, then i goes from 1 to 3 in the sum above.

If $Q$ is small, that means that the attribute is not relevant -- the data in each split are following the same distribution as the data before splitting on this attribute. If $Q$ is large, that means that there is a lot of "error" between what we would have expected (under the irrelevant attribute hypothesis) and the actual distribution of examples.

The $\chi^2$ distribution will determine the probability that the attribute is not relevant. I have provided a Scheme implementation of this function in the support code: 

  (chi^2 dof Q)
You should use 
dof = (number of values of this attribute) - 1

The chi^2 procedure will return a probability between 0 and 1 which indicates that our hypothesis (that this attribute doesn't matter) is correct. We will set a low threshold for this test: if the probability is greater than 0.001, then we will assume that the hypothesis is correct.

Although this threshold may seem low, consider the following quote from "Numerical Recipes in C"

It is not uncommon to deem acceptable on equal terms any models with, say, Q > 0.001. This is not as sloppy as it sounds: truly wrong models will often be rejected with vastly smaller values of Q, 1e-18, say.

If the "irrelevance hypothesis" is deemed correct, then you should not split on this attribute -- instead just pick the majority classification.

For your information, my Scheme implementation of the chi^2 function follows the algorithm from the book "Numerical Recipes in C" for computing the gammq function.

Problem 4: testing and comparison

 For this (written) problem, turn in the following:

  1. Plot a learning curve (as described below) using your learn-dtree procedure.

  2. Run your learn-dtree and chi^2-learn-dtree procedures on the loan-data and the mushroom-data1. Show the resulting decision trees and explain the difference(s) between the trees learned with and without the chi-squared pruning. You should go into some detail, but your answer should not exceed 2 pages. You should be able to answer this part of Problem 4 in 1 page, though.

Learning curves

In order to plot learning curves, you should repeat the following for actual training data set sizes of 5, 10, 15, 20, 50, 80, 110, 140, 170, and 200.

You should find it simple to write a procedure to help you run these tests. Show the performance on the training data and the testing data on the same plot. (The x axis should be the data set size, and the y axis should be the fraction of examples classified correctly. There should be two curves on the plot: one for performance on the training data and one for the testing data.)

(Bonus) Problem 5: discretize

 For this problem: