Lecture 15 — Sets¶
Overview¶
- Example: finding all individuals listed in the Internet Movie Database (IMDB)
- A solution based on lists
- Sets and set operations
- A solution based on sets.
- Efficiency and set representation
Reading is Section 9.1 of Practical Programming, as well as the last part of Section 5.10 on command-line arguments.
Finding All Persons in the IMDB file¶
We are given a file extracted from the Internet Movie Database (IMDB) called
imdb_data.txtcontaining, on each line, a person’s name, a movie name, and a year. For example,Kishiro, Yukito | Battle Angel | 2016
Goal:
- Find all persons named in the file
- Count the number of different persons named.
- Ask if a particular person is in the set
The challenge in doing this is that many names appear multiple times.
First solution: store names in a list. We’ll start from the following code, posted on-line in
lec15_find_names_start.pyimdb_file = raw_input("Enter the name of the IMDB file ==> ").strip() name_list = [] for line in open(imdb_file): words = line.strip().split('|') name = words[0].strip()
and complete the code in class.
The challenge is that we need to check that a name is not already in the list before adding it.
How To Test?¶
- The file
imdb_data.txthas about 260K entries. How will we know our results are correct? - Even if we restrict it to movies released in 2010-2012 (the file
imdb_2010-12.txt), we still have 25K entries! - We need to generate a smaller file with results we can test by hand
- I have generated
hanks.txtfor you and will use it to test our program before testing on the larger files.
- I have generated
What Happens?¶
- Very slow on the large files because we need to scan through the list to see if a name is already there.
- We’ll write a faster implementation based on Python sets.
- We’ll start with the basics of sets.
Sets¶
- A Python set is an implementation of the mathematical notion of a
set:
- No order to the values (and therefore no indexing)
- Contains no duplicates
- Contains whatever type of values we wish; including values of different types.
- Python set methods are exactly what you would expect.
- Each has a function call syntax and many have operator syntax in addition.
Set Methods¶
Initialization comes from a list, a range, or from just
set():>>> s1 = set() >>> s1 set([]) >>> s2 = set(range(0,11,2)) >>> s2 set([0, 2, 4, 6, 8, 10]) >>> v = [4, 8, 4, 'hello', 32, 64, 'spam', 32, 256] >>> s3 = set(v) >>> s3 set([32, 64, 4, 'spam', 8, 256, 'hello'])
The actual methods are
s.add(x)— add an element if it is not already theres.clear()— clear out the set, making it emptys1.difference(s2)— create a new set with the values froms1that are not ins2. Using Python’s operator syntax this iss1 - s2
s1.intersection(s2)— create a new set that contains only the values that are in both sets. Operator syntax:s1 & s2
s1.union(s2)— create a new set that contains values that are in either set. Operator syntax:s1 | s2
s1.issubset(2)—- are all elements ofs1also ins2? Operator syntax:s1 <= s2
s1.issuperset(s2)— are all elements ofs2also ins1? Operator syntax:s1 >= s2
s1.symmetric_difference(s2)— create a new set that contains values that are ins1ors2but not in both.s1 ^ s2
We will explore the intuitions behind these set operations by considering
s1to be the set of actors in comedies,s2to be the set of actors in action movies
and then consider who is in the sets
s1 - s2 s1 & s2 s1 | s2 s1 ^ s2
Exercises¶
Sets should be relatively intuitive, so rather than demo them in class, we’ll work through these as an exercise:
>>> s1 = set(range(0,10)) >>> s1 >>> s1.add(6) >>> s1.add(10) >>> s2 = set(range(4,20,2)) >>> s2 >>> s1 - s2 >>> s1 & s2 >>> s1 | s2 >>> s1 <= s2 >>> s3 = set(range(4,20,4)) >>> s3 <= s2
Back to Our Problem¶
- We’ll modify our code to find the actors in the IMDB. The code is actually very simple and only requires a few set operations.
Side-by-Side Comparison of the Two Solutions¶
- Neither the set nor the list is ordered. We fixed this at the end by
sorting.
- The list can be sorted directly.
- The set must be converted to a list first. The function
sorteddoes this for us.
- What about speed? The set version is MUCH FASTER — to the point
that the list version is essentially useless on a large data set.
- We’ll explore why in the rest of this lecture.
Comparison of Running Times for Our Two Solutions¶
- List-based solution:
- Each time before a name is added, the code — through the method
in— scans through the entire list to decide if it is there. - Thus, the work done is proportional to the size of the list.
- The overall running time is therefore roughly proportional to the
squareof the number of entries in the list (and the file). - Letting the mathematical variable
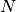 represent the length
of the list, we write this more formally as
represent the length
of the list, we write this more formally as 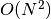 , or
“the order of N squared”
, or
“the order of N squared”
- Each time before a name is added, the code — through the method
- Set-based code
- For sets, Python uses a technique called hashing to restrict the
running time of the
addmethod so that it is independent of size of the set.- The details of hashing are covered in CSCI 1200, Data Structures.
- The overall running time is therefore roughly proportional to the length of the set (and number of entries in the file).
- We write this as
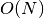 .
.
- For sets, Python uses a technique called hashing to restrict the
running time of the
- We will discuss this type of analysis more later in the semester.
- It is covered in much greater detail in Data Structures and again in Intro. to Algorithms.
Discussion¶
- Python largely hides the details of the containers — set and list in this case — and therefore it is hard to know which is more efficient and why.
- For programs applied to small problems involving small data sets, efficiency rarely matters.
- For longer programs and programs that work on larger data sets,
efficiency does matter, sometimes tremendously. What do we do?
- In some cases, we still use Python and choose the containers and operations that make the code most efficient.
- In others, we must switch to programming languages, such as C++, that generate and use compiled code.
Summary¶
- Sets in Python realize the notion of a mathematical set, with all the associated operations.
- Operations can be used as method calls or, in many cases, operators.
- The combined core operations of finding if a value is in a set and adding it to the set are much faster when using a set than the corresponding operations using a list.
- We will continue to see examples of programming with sets when we work with dictionaries.
Practice Problems¶
These practice problems are to be used both in understanding sets and as a study aid for the next test.
What is the output of the following Python code? Write the answer by hand before you type it into the Python interpreter. Do not worry about getting the order of the values in a set correct:
>>> s1 = set([0,1,2]) >>> s2 = set(range(1,9,2)) >>> print 'A:', s1.union(s2) >>> print 'B:', s1 >>> s1.add('1') >>> s1.add(0) >>> s1.add('3') >>> s3 = s1 | s2 >>> print 'C:', s3 >>> print 'D:', s3 - s1
Note that this example does NOT cover all of the possible set operations. You should generate and test your own examples to ensure that you understand all of the basic set operations.
Write Python code that implements the following set functions using a combination of loops, the
inoperator, and theaddfunction. In each case,s1ands2are sets and the function call should return a set.union(s1,s2)intersection(s1,s2)symmetric_difference(s1,s2)
Write a Python function to find all of the family names in the IMDB data set. Output them in alphabetical order. Assume the family name ends with the first
','on each input line. Would you have noticed a significant difference in execution time if we used a list implementation? What if the data set were just the students in this class, or all students at RPI?