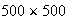 .
When solving for an
.
When solving for an
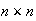 grid of points, the space complexity is
grid of points, the space complexity is
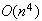 ,
and the time complexity is
,
and the time complexity is
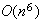 .
We would like to do better than this.
.
We would like to do better than this.
ODETLAP Tiling
by Dan TracyApril 26, 2007
Given a matrix of terrain elevations, we can easily render it as an image in
OpenGL. The simplest approach is to use GL_TRIANGLES to linearly interpolate
the space between the grid points. However, this results in a very blocky
image. We could generate a smoother terrain by adding more grid points and
interpolating them with a nonlinear method. One such method is ODETLAP
(http://www.ecse.rpi.edu/Homepages/wrf/pmwiki/Research/AlternateTerrainReps#toc16),
developed by W.R. Franklin. However, the current implementation does not work
efficiently on grids larger than
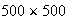 .
When solving for an
.
When solving for an
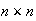 grid of points, the space complexity is
grid of points, the space complexity is
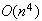 ,
and the time complexity is
,
and the time complexity is
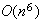 .
We would like to do better than this.
.
We would like to do better than this.
The original ODETLAP formulation:
Given a
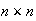 grid
grid
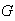 ,
where some
,
where some
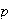 grid points have known values, and the rest
(
grid points have known values, and the rest
(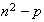 grid points) are unknown. We can transform the matrix
grid points) are unknown. We can transform the matrix
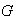 into a vector
into a vector
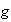 of size
of size
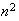 .
We produce a system of linear equations by setting the value of each point
equal to the average of its four neighbors (or fewer than four for boundary
points). Then additional equations are produced by setting each known grid
point equal to its known value. This results in an overdetermined system of
linear equations. There are
.
We produce a system of linear equations by setting the value of each point
equal to the average of its four neighbors (or fewer than four for boundary
points). Then additional equations are produced by setting each known grid
point equal to its known value. This results in an overdetermined system of
linear equations. There are
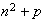 equations for
equations for
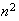 unknowns.
unknowns.
The known points are allowed to change in order to produce a smoother result.
The first set of equations is multiplied a smoothness parameter
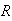 .
This specifies the relative weight between the first set of equations, which
enforce the smoothness of the solution, and the second set of equations, which
enforce the accuracy of the known points. For values of
.
This specifies the relative weight between the first set of equations, which
enforce the smoothness of the solution, and the second set of equations, which
enforce the accuracy of the known points. For values of
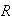 close to
close to
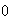 ,
the values of the known points will stay relatively fixed. For larger values
of
,
the values of the known points will stay relatively fixed. For larger values
of
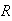 ,
the known points may drift in order to produce a smoother solution. As
,
the known points may drift in order to produce a smoother solution. As
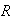 approaches
approaches
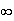 ,
the solution approaches a flat plane.
,
the solution approaches a flat plane.
The system of equations can be expressed as
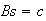 ,
where
,
where
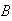 is of size
is of size
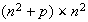 ,
and
,
and
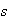 and
and
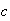 are each of size
are each of size
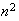 .
This system was solved with some MATLAB code, which I obtained from Zhongyie
Xie.
.
This system was solved with some MATLAB code, which I obtained from Zhongyie
Xie.
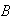 is formed with MATLAB's sparse data structure, so its storage requirement is
only
is formed with MATLAB's sparse data structure, so its storage requirement is
only
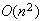 .
However, solving the matrix equation will still require
.
However, solving the matrix equation will still require
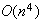 storage.
storage.
I eliminated the smoothness parameter and the second set of equations by
absorbing them into the first set of equations. The known points are no longer
treated as variables. In the equations, the variables for the known points are
replaced by their known constants. I now have
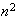 equations for
equations for
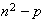 unknowns. The solution of this system corresponds to the solution of the
original ODETLAP algorithm as
unknowns. The solution of this system corresponds to the solution of the
original ODETLAP algorithm as
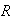 approaches
approaches
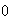 .
.
Next I focused on a special case: Given an
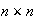 terrain of elevations, with every grid point known, expand the terrain to a
higher resolution
(
terrain of elevations, with every grid point known, expand the terrain to a
higher resolution
(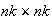 )
by inserting
)
by inserting
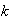 unknown points between each of the known points. This new terrain can then be
partitioned into
unknown points between each of the known points. This new terrain can then be
partitioned into
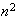 subgrids of size
subgrids of size
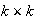 so that the four corners of each subgrid are known. Each known point would
belong to four subgrids (except the boundary points). Each subgrid can then be
solved separately, and their solutions stitched together afterwards. For each
point that belongs to more than one subgrid, the solutions are averaged
together. In this manner, we can avoid the
so that the four corners of each subgrid are known. Each known point would
belong to four subgrids (except the boundary points). Each subgrid can then be
solved separately, and their solutions stitched together afterwards. For each
point that belongs to more than one subgrid, the solutions are averaged
together. In this manner, we can avoid the
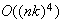 space complexity that the original ODETLAP incurs. However, this produces a
less smooth solution than the original ODETLAP.
space complexity that the original ODETLAP incurs. However, this produces a
less smooth solution than the original ODETLAP.
A further approach is to use subgrids of size
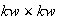 .
The number of subgrids is still
.
The number of subgrids is still
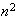 ,
so there is considerable overlap between the subgrids. Like before, for each
point that belongs to more than one subgrid, the solutions are averaged
together. This produces a smoother solution, though with a higher cost.
,
so there is considerable overlap between the subgrids. Like before, for each
point that belongs to more than one subgrid, the solutions are averaged
together. This produces a smoother solution, though with a higher cost.
Now we must measure the tradeoff of efficiency vs. accuracy of the new
methods. Efficiency can be measured with cpu time. For accuracy, we can
compute the solution
(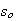 )
with the original ODETLAP as well as the solution
(
)
with the original ODETLAP as well as the solution
(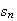 )
with the new method. The error vector is then
)
with the new method. The error vector is then
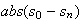 .
From this, I extracted the maximum and the average error. However, there may
be large examples where we can compute the solution with the new method, but
it is not feasible to compute the solution with the original ODETLAP. In this
case, we can examine the residual of the overdetermined system instead:
.
From this, I extracted the maximum and the average error. However, there may
be large examples where we can compute the solution with the new method, but
it is not feasible to compute the solution with the original ODETLAP. In this
case, we can examine the residual of the overdetermined system instead:
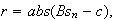 where
where
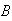 and
and
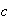 correspond to the equations generated by the original ODETLAP. However, there
does not usually exist a solution such that
correspond to the equations generated by the original ODETLAP. However, there
does not usually exist a solution such that
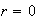 ,
so it is more difficult to determine how close we are to the best solution.
But we can compare competing methods against each other this way. Also, this
residual corresponds to the "sharpness" of the solution in terms of the
elevation units of the original data.
,
so it is more difficult to determine how close we are to the best solution.
But we can compare competing methods against each other this way. Also, this
residual corresponds to the "sharpness" of the solution in terms of the
elevation units of the original data.
An iterative scheme of solving the overdetermined system of equations could be
greatly beneficial. Using the previous method, we can make a very good initial
guess into the algorithm. Using the notation that
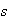 is the computed solution, and
is the computed solution, and
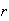 is the residual
is the residual
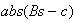 ,
we should be able to compute the Jacobian matrix
,
we should be able to compute the Jacobian matrix
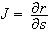 .
The original ODETLAP will give us the solution that minimizes the residual, so
that
.
The original ODETLAP will give us the solution that minimizes the residual, so
that
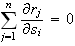 for every
for every
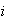 .
This could be used in a scheme like Newton's method, but I have not been able
to complete the algorithm.
.
This could be used in a scheme like Newton's method, but I have not been able
to complete the algorithm.
In the numerical experiments, I used the
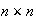 upper-left corner of the Lake Champlain data set. Then I ran the ODETLAP to
produce a higher resolution
upper-left corner of the Lake Champlain data set. Then I ran the ODETLAP to
produce a higher resolution
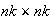 terrain. The values chosen for
terrain. The values chosen for
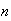 and
and
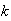 are reported in the table. I compared the results from different values of
are reported in the table. I compared the results from different values of
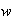 ,
the size of the subgrids, against the results from the original ODETLAP. The
tables are at the end of the paper.
,
the size of the subgrids, against the results from the original ODETLAP. The
tables are at the end of the paper.
The residuals are quite large when
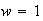 ,
though not unreasonable. However, the results start to look very good at
,
though not unreasonable. However, the results start to look very good at
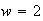 .
That is, the residual from
.
That is, the residual from
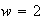 is on the same order of magnitude as the residual from the original ODETLAP.
And there is considerable speedup. For example, for
is on the same order of magnitude as the residual from the original ODETLAP.
And there is considerable speedup. For example, for
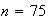 ,
,
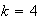 ,
the original ODETLAP takes 233 seconds, and the
,
the original ODETLAP takes 233 seconds, and the
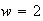 method takes 11.5 seconds, while the maximum residual only increases from 1.89
to 2.07, and the average residual only increases from 0.0865 to 0.0875. When
rendered, these differnce should hardly be noticeable. We now have a very
efficient and practical interpolative scheme.
method takes 11.5 seconds, while the maximum residual only increases from 1.89
to 2.07, and the average residual only increases from 0.0865 to 0.0875. When
rendered, these differnce should hardly be noticeable. We now have a very
efficient and practical interpolative scheme.
Tiling demonstration
The intersections of the solid blue lines are the known points. The intersections of the dotted blue lines are the unknown points. The red boxes are the tiles that ODETLAP is performed on.

I downsampled the Lake Champlain data to 100×100:

Then I expanded it to a 400×400 grid using my tiled ODETLAP scheme:

The tiled scheme took 23 seconds to compute. The original untiled scheme took 15 minutes to compute.
References:
http://www.ecse.rpi.edu/Homepages/wrf/pmwiki/Research/AlternateTerrainReps#toc16
Numerical results: n=15, k=6 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 2.48e+000 0.00e+000 0.00e+000 8.77e-001 5.52e-002 w=1 1.48e+000 2.91e+000 3.66e-001 1.26e+000 7.36e-002 w=2 2.02e+000 1.37e+000 1.56e-001 1.05e+000 5.83e-002 w=3 3.39e+000 9.12e-001 1.20e-001 1.03e+000 5.81e-002 w=4 5.47e+000 9.41e-001 1.08e-001 1.03e+000 5.83e-002 w=5 8.27e+000 9.30e-001 1.02e-001 1.03e+000 5.90e-002 w=6 1.03e+001 9.31e-001 1.01e-001 1.03e+000 5.96e-002 w=7 1.29e+001 9.31e-001 1.05e-001 1.03e+000 6.00e-002 w=8 1.64e+001 9.31e-001 1.11e-001 1.03e+000 6.01e-002 w=9 1.59e+001 9.31e-001 1.01e-001 1.03e+000 5.97e-002 w=10 1.66e+001 9.31e-001 8.99e-002 1.03e+000 5.90e-002 n=20, k=6 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 6.88e+000 0.00e+000 0.00e+000 7.28e-001 4.47e-002 w= 1 2.70e+000 2.75e+000 3.06e-001 1.26e+000 6.05e-002 w= 2 3.91e+000 1.05e+000 1.29e-001 8.78e-001 4.72e-002 w= 3 6.88e+000 9.12e-001 1.03e-001 8.37e-001 4.72e-002 w= 4 1.27e+001 7.81e-001 8.96e-002 8.07e-001 4.73e-002 w= 5 1.90e+001 8.21e-001 8.44e-002 7.92e-001 4.77e-002 w= 6 2.84e+001 8.16e-001 8.37e-002 7.81e-001 4.82e-002 w= 7 3.36e+001 8.16e-001 8.42e-002 8.02e-001 4.83e-002 w= 8 4.82e+001 8.16e-001 8.58e-002 7.87e-001 4.84e-002 n=30, k=4 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 1.20e+001 0.00e+000 0.00e+000 1.51e+000 8.75e-002 w= 1 5.66e+000 2.64e+000 2.45e-001 2.13e+000 9.74e-002 w= 2 6.81e+000 1.04e+000 1.03e-001 1.59e+000 8.89e-002 w= 3 9.61e+000 7.91e-001 7.94e-002 1.52e+000 8.88e-002 w= 4 1.35e+001 6.75e-001 6.65e-002 1.51e+000 8.89e-002 w= 5 2.00e+001 6.92e-001 6.13e-002 1.51e+000 8.95e-002 w= 6 2.89e+001 6.88e-001 5.93e-002 1.51e+000 8.98e-002 w= 7 3.93e+001 6.88e-001 5.95e-002 1.51e+000 9.01e-002 w= 8 5.14e+001 6.88e-001 6.08e-002 1.51e+000 9.02e-002 new machine: n=50, k=4 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 4.71e+01 0.00e+00 0.00e+00 1.89e+00 9.08e-02 w= 1 2.36e+00 3.58e+00 2.63e-01 3.09e+00 1.01e-01 w= 2 4.98e+00 1.67e+00 1.13e-01 2.07e+00 9.18e-02 w= 3 9.90e+00 1.14e+00 8.26e-02 2.05e+00 9.13e-02 w= 4 1.60e+01 1.11e+00 6.70e-02 2.00e+00 9.13e-02 w= 5 2.57e+01 1.11e+00 5.97e-02 1.98e+00 9.16e-02 w= 6 3.97e+01 1.10e+00 5.58e-02 1.97e+00 9.18e-02 w= 7 6.14e+01 1.10e+00 5.33e-02 1.96e+00 9.19e-02 n=60, k=4 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 8.83e+01 0.00e+00 0.00e+00 1.89e+00 9.21e-02 w= 1 3.63e+00 4.09e+00 2.72e-01 3.09e+00 1.03e-01 w= 2 8.05e+00 1.83e+00 1.17e-01 2.07e+00 9.33e-02 w= 3 1.33e+01 1.22e+00 8.32e-02 2.05e+00 9.27e-02 w= 4 2.15e+01 1.11e+00 6.53e-02 2.00e+00 9.26e-02 w= 5 3.85e+01 1.11e+00 5.66e-02 1.98e+00 9.29e-02 w= 6 5.96e+01 1.10e+00 5.19e-02 1.97e+00 9.31e-02 n=75, k=4 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 2.33e+02 0.00e+00 0.00e+00 1.89e+00 8.65e-02 w= 1 6.25e+00 4.09e+00 2.56e-01 3.09e+00 9.70e-02 w= 2 1.15e+01 1.83e+00 1.11e-01 2.07e+00 8.75e-02 w= 3 1.88e+01 1.27e+00 7.86e-02 2.05e+00 8.68e-02 w= 4 3.43e+01 1.18e+00 6.16e-02 2.00e+00 8.68e-02 w= 5 6.16e+01 1.14e+00 5.32e-02 1.98e+00 8.70e-02 w= 6 9.62e+01 1.11e+00 4.83e-02 1.97e+00 8.72e-02 w= 7 1.51e+02 1.10e+00 4.51e-02 1.96e+00 8.73e-02 n=85, k=4 Method Time Max_Error Avg_Error Max_Residual Avg_Residual orig 3.64e+02 0.00e+00 0.00e+00 1.89e+00 8.74e-02 w= 1 8.78e+00 4.09e+00 2.58e-01 3.09e+00 9.84e-02 w= 2 1.27e+01 1.83e+00 1.12e-01 2.07e+00 8.82e-02 w= 3 2.43e+01 1.22e+00 7.83e-02 2.05e+00 8.74e-02 w= 4 4.47e+01 1.11e+00 6.07e-02 2.00e+00 8.73e-02 w= 5 8.20e+01 1.11e+00 5.11e-02 1.98e+00 8.75e-02