Skip to main content

Homework 1: Convex Hulls

Part 1: Book Problems

Prepare a PDF file named hw1_convex_hulls.pdf with your answers to the book problems below. You may use Latex, Google Docs (export/save as PDF), MS Word (export/save as PDF), and/or legibly handwrite on paper and scan to PDF.

From "Computational Geometry: Algorithms and Applications", de Berg, Cheong, van Kreveld, and Overmars.

You may discuss these problems with your classmates, but you must write up your solutions individually. Note the names of anyone you talked to or collaborated with in your hw1_convex_hulls.pdf writeup.

Please do not search for solutions or notes published by the authors or any instructor or notes or solutions shared by other students on the internet. Any use of these types of materials is considered a violation of Academic Integrity for this course.

1.3
Let E be an unsorted set of n segments that are the edges of a convex polygon. Describe an O(n log n) algorithm that computes from E a list containing all vertices of the polygon, sorted in clockwise order.

1.7 a,c,d
Consider the following alternative approach to computing the convex hull of a set of points in the plane: We start with the rightmost point. This is the first point p1 of the convex hull. Now imagine that we start with a vertical line and rotate it clockwise until it hits another point p2. This is the second point on the convex hull. We continue rotating the line but this time around p2 until we hit a point p3. In this way we continue until we reach p1 again.
a. Give pseudocode for this algorithm.
c. Prove that the algorithm correctly computes the convex hull.
d. Prove that the algorithm can be implemented to run in time O(n * h), where h is the complexity of the convex hull.

1.9
Suppose that we have a subroutine CONVEXHULL available for computing the convex hull of a set of points in the plane. Its output is a list of convex hull vertices, sorted in clockwise order. Now let S = {x1,x2,...,xn} be a set of n numbers. Show that S can be sorted in O(n) time plus the time needed for one call to CONVEXHULL. Since the sorting problem has an Omega(n log n) lower bound, this implies that the convex hull problem has an Omega(n log n) lower bound as well. Hence, the algorithm presented in this chapter is asymptotically optimal.

Part 2: Install CGAL & Qt

CGAL, the Computational Geometry Algorithms Library, is an open-source software project to provide efficient and reliable implementations of many important geometric data structures and algorithms. We'll also use the open-source edition of Qt, a C++ graphical user interface (GUI) toolkit. Both CGAL and Qt are available for Linux, MacOS, and Windows.

  1. Install CGAL & Qt on your laptop or desktop.
    https://doc.cgal.org/latest/Manual/general_intro.html

    See also additional Programming Environment information.

  2. Download the CGAL demos & examples.
    https://github.com/CGAL/cgal/releases/download/v5.3.1/CGAL-5.3.1-examples.tar.xz

  3. Compile & run a few of these programs to confirm that your system is correctly installed & functional. There are lots of examples (these programs generally do not have a Qt graphical user interface) and demos (these programs generally do have an interactive Qt graphics user interface).

    Specifically, we suggest that you start with:

    Please use the Submitty Discussion Forum to ask questions about installation, compilation, and testing of these examples.

Part 3: CGAL Programming Task

Given a set of n input points on the 2D xy plane and floating point value for the maximum desired perimeter, devise and implement a polynomial-time, greedy algorithm to find the largest subset of of those original n points whose convex hull is less than or equal to the specified perimeter. Remember that a greedy algorithm is incremental, and will make an optimal choice at each step as it attempts to find the overall solution to the entire problem. However, it is not guaranteed to find the overall optimal solution.

For example, given the following input file with the following seven points visualized on the right:

input.txt 

      
  0.0 0.0
  2.0 0.0
  1.0 10.0
  0.0 2.0
  10.0 1.0
  2.0 2.0
  1.0 1.0


If we run the program with these four command line arguments: 

      
  ./convex_hull_subset_perimeter input.txt 8.1 output_subset.txt output_hull.txt

On the right we visualize the solution, a subset of five of the input points, whose convex hull perimeter = 8.0, represented in the output files below:

output_subset.txt - a subset of the input points 
      
  0.0 0.0
  2.0 0.0
  0.0 2.0
  2.0 2.0
  1.0 1.0
output_hull.txt - the convex hull of that subset of points 
      
  0.0 0.0
  2.0 0.0
  2.0 2.0
  0.0 2.0

And below we visualize a few more examples solutions for the same input file, but with for different command-line-specified maximum perimeters (33.0, 23.0, and 7.0, respectively):

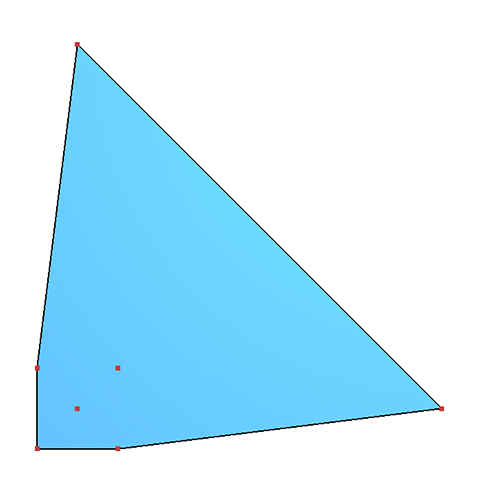
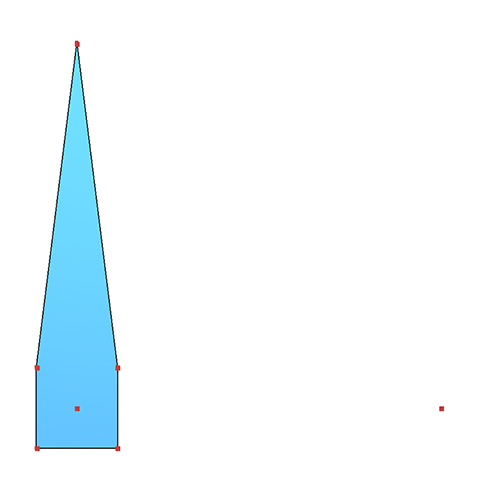
Your task is to write a new C++ program using CGAL and Qt, and learn some of the basics of this powerful open-source library for computational geometry. You are encouraged to use the CGAL/Qt draw routines found in the CGAL demos and examples for visualization and debugging, but your finished program is not required to incorporate any specific visual output.

Here is a Sample CMakeLists.txt file that you may use for this assignment. It expects a single C++ source code file named convex_hull_subset_perimeter.cpp and builds with the CGAL and Qt5 libraries to produce an executable named convex_hull_subset_perimeter. You are welcome to modify this file as necessary for your solution.

Your program should find a good, valid solution for the input point file and command-line specified maximum perimeter. But it is not necessarily the optimal solution -- there may be a different, larger subset (with more points) that also meets the specified maximum convex hull perimeter requirement. You are not expected to develop or implement an optimal algorithm.

Make up additional input files to test your program. Submitty autograding will be configured to run your program against both small and moderate-sized input files.

Part 4: Analysis

In your convex_hulls.pdf file, analyze (Big O Notation + brief justification) the running time of the greedy algorithm you designed and implemented in Part 3. For your analysis, assume your input file contains n points, the subset solution output by your program consists of s points and the (one or more) convex hulls computed in running your program approximately h points.

Part 5: Robustness and Optimality - OPTIONAL Extra Credit

For extra credit explore the accuracy, robustness, and optimality of your algorithm and implementation. It's ok that your algorithm and/or implementation is fragile (inaccurate and/or not robust). In your convex_hulls.pdf file, discuss and/or construct and test specific inputs to expose these flaws. Are there inputs and command line arguments for which your program may crash or fail to produce an output? Are there inputs for which your program produces a valid solution, but it is not optimal? Construct a specific input file for which your program produces a good, valid solution, but that solution is not optimal. Manually construct the optimal solution for this input. Discuss why your greedy algorithm does not find this solution. Describe a brute-force (and much more computationally-expensive) algorithm that would be guaranteed to find the solution for this input, and all inputs. Analyze the running time of this brute-force algorithm that is guaranteed to find the optimal, maximum size subset solution.