Lecture 6 — Decisions

Overview — Logic and Decision Making

• Boolean logic
• Use in decision making
• Use in branching and alternatives

Reading: Sections 6.1 and 6.2 of Practical Programming. We’ll return to the rest of this chapter later in the semester.

Part 1: Boolean Values

• Yet another type

• Values are True and False

• We’ll see a large series of operations that either produce or use boolean values, including relational operators such as <, <=, etc. and logical operations such as and and or.

• We can assign them to variables, as in,

  x = True
  

  but we will not explore this until Lecture 9.

Relational Operators — Less Than and Greater Than

• Comparisons between values, perhaps values associated with variables, to produce a boolean outcome.

• For numerical values, <, <=, >, >= are straightforward:

  >>> x = 17
  >>> y = 15.1
  >>> x < y
  False
  >>> x <= y
  False
  >>> x <= 17
  True
  >>> y < x
  True
  

• The comparison operators <, <=, >, >= may also be used for strings but the results are sometimes a bit surprising:

  >>> s1 = 'art'
  >>> s2 = 'Art'
  >>> s3 = 'Music'
  >>> s4 = 'music'
  >>> s1 < s2
  False
  >>> s2 < s3
  True
  >>> s2 < s4
  True
  >>> s1 < s3
  False
  

• With strings, the ordering is what’s called lexicographic rather than purely alphabetical order:

  • All capital letters come before small letters, so strict alphabetical ordering can only be ensured when there is no mixing of caps and smalls.

Relational Operators: Equality and Inequality

• Testing if two values are equal uses the combined, double-equal symbol == rather than the single =, which is reserved for assignment.
  • Getting accustomed to this convention requires practice, and is a common source of mistakes
• Inequality is indicated by !=.
• We will play with a few examples in class.

Part 1 Exercises

1. What are the values of the following boolean expressions?

   a = 1.6
   b = -1.7
   c = 15
   s = 'hi'
   t = "good"
   u = "Bye"
   v = "GOOD"
   w = "Bye"
   
   a < b             # A
   a < abs(b)        # B
   a >= c            # C
   s < t             # D
   t == v            # E
   u == w            # F
   b < y             # G
   

2. What happens with the following?

   u == w
   u = v
   u == w
   

Part 2: if Statements

• General form of what we saw in the example we explored at the start of lecture:

  if condition:
     block1
  else:
     block2
  

  where

  • condition is the result of a logical expression, such as the result of computing the value of a relational operation
  • block1 is Python code executed when the condition is True
  • block2 is Python code executed when the condition is False

• All statements in the block1 and block2 must be indented the same number of spaces

• The block continues until the indentation stops, and returns to the same level of indentation as the statement starting with if

• The else: and block2 are optional, as the following example shows.

Example: Heights of Siblings

• Suppose we want to input the heights of two siblings and output the name and height of the taller of them.

• We could write two consecutive if statements:

  name1 = "Dale"
  print "Enter the height of %s in cm ==> " %name1,
  height1 = int(raw_input())
  
  name2 = "Erin"
  print "Enter the height of %s in cm ==> " %name2,
  height2 = int(raw_input())
  
  if height1 < height2:
      print "%s is taller" %name2
      max_height = height2
  
  if height1 >= height2:
      print "%s is taller" %name1
      max_height = height1
  
  print "The max height is %d" %max_height
  

• Since the two if statements are (seemingly) exclusive, we can use the if-else structure to simplify this:

  name1 = "Dale"
  height1 = int(raw_input("Enter the height of %s in cm ==> " %name1))
  
  name2 = "Erin"
  height2 = int(raw_input("Enter the height of %s in cm ==> " %name2,))
  
  max_height = 0;
  
  if height1 < height2:
      print "%s is taller" %name2
      max_height = height2
  else:
      print "%s is taller" %name1
      max_height = height1
  
  print "The max height is %d" %max_height
  

• Note that none of the blank lines are required for these programs to have correct syntax.

• Note also that neither program handles the case of Dale and Erin being the same height. For this we need the next Python construct.

Elif

Recall the kids guessing game where someone thinks of a number and you have to guess it. The only information you are given is that the person who knows the number tells you if your guess is too high, too low, or if you got it correct.

• When we have three or more alternatives to consider we use the if-elif-else structure:

  if condition1:
      block1
  elif condition2:
      block2
  else:
      block3
  

• We’ll write the solution and discuss the flow of Python execution in class.

• Notes:

  • You can use multiple elif conditions and blocks
  • You do NOT need to have an else block.
  • Exactly one block of code (block1, block2, block3) is executed!
  • If we leave off the else: and block3, then it is possible that none of the blocks are executed.

Part 2 Exercise

1. Rewrite the height example to use elif to handle the case of Dale and Erin having the same height.

Part 3: More Complex Boolean Expressions, Starting with and

Consider the following piece of Python code:

if cel > 0 and cel < 100:
    print "At %dC water is liquid" %cel

• A boolean expression involving and is True if and only if both the relational operations produce the value True

More Complex Boolean Expressions — or

Consider the following:

if cel < 0 or cel > 100:
    print "At %dC water is not a liquid" %cel

• The boolean expression is True if ANY of the following occurs

  • the left relational expression is True,
  • the right relational expression is True,
  • both the left and right relational expression are True.

• This is called the inclusive or and it is somewhat different from common use of the word or in English.

• For examples, in the sentence

  You may order the pancakes or the omlet.

  usually means you may choose pancakes, or you may choose an omelet, but you may not choose both (unless you pay extra).

  • This is called the exclusive-or; it is only used in logic and computer science in very special cases.
  • Hence, or always means inclusive-or.

Boolean Logic — not

• We can also “logically negate” a boolean expression using not.

  a = 15
  b = 20
  if not a<b:
      print "a is not less than b"
  else:
      print "a is less than b"
  

Part 3 Exercises

1. What are the results of the following Python boolean expressions:

   >>> x = 15
   >>> y = -15
   >>> z = 32
   >>> x == y and y < z        #A
   >>> x == y or y < z         #B
   >>> x == abs(y) and y < z   #C
   >>> x == abs(y) or y < z    #D
   >>> not x == abs(y)         #E
   >>> not x != abs(y)         #F
   

2. Suppose the bounds of a rectangle are defined by

   x0 = 10
   x1 = 16
   y0 = 32
   y1 = 45
   

   Note that a point at location 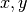is inside the rectangle if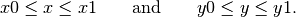

   

   1. Write a Python boolean expression using and that is True if a point is inside the rectangle.
   2. Write a Python boolean expression using or that is True if a point is outside the rectangle.

Summary and Looking Ahead

• if-else and if-elif-else are tools for making decisions and creative alternative computations and results
• The conditional tests involve relationship operators and logical operators
  • Be careful of the distinction between = and ==
• In Lecture 9 we will review boolean logic and discuss more complex if structures.