Lecture 9 — Decisions Part 2

Overview — Logic and Decision Making, part 2

• Logic is the key to getting programs right
• Boolean logic
• Nested if statements
• Assigning booelan variables

Before we start, let’s have a chat first

Programming requires four basic skills:

1. Develop a solution.
   • Start with small steps, solve them and then add complexity
2. Structure your code.
   • Abstract out repeated code into functions.
   • Make your code easy to read and modify. Use meaningful variable names and break complex operations into smaller parts.
   • Do not hard code values so that it is easy to change the program.
   • Include comments for important functions, but do not clutter your code with unnecessary comments. If a function makes an assumption on validity or type of inputs, this is a good thing to document in your code.
   • If your function is meant to return a value, make sure it always returns a value.
3. Test your code.
   • Find all possible cases that your program should work for. As programs get larger, this is increasing hard.
   • If you cannot check for all inputs, then you must then check your code for meaningful inputs: regular (expected inputs) and edge cases (inputs that can break your code).
4. Debug your code.
   • Never assume an untested part of your code is bug free.
   • Learn syntax well so that you can spot and fix syntax errors fast.
   • Semantic errors are much harder to find and fix. You need strategies to isolate where the error is.
   • Print output before and after crucial steps.
   • Look at where your program crashed.
   • Use a debugger.
   • Simplify the problem. Remove parts of your code until you no longer have error.
   • Test parts of your code separately and once you are convinced they are bug free, concentrate on other parts.

We will attempt to write an unbreakable program in today’s lecture.

Part 1: Boolean Logic

• Invented / discovered by George Boole in the 1840’s to reduce classical logic to an algebra
  • This was a crucial mathematical step on the road to computation and computers.
• Values (in Python) are True and False
• Operators
  • Comparisons: <, >, <=, >=, == !=
  • Logic: and, or, not

Truth Tables

• Aside to recall the syntax: and,or,not are lower case!

• If we have two boolean expressions, which we will refer to as ex1 and ex2, and if we combine their “truth” values using and we have the following “truth table” to describe the result

  ex1	ex2	ex1 and ex2
  False	False	False
  False	True	False
  True	False	False
  True	True	True

• If we combine the two expressions using or, we have

  ex1	ex2	ex1 or ex2
  False	False	False
  False	True	True
  True	False	True
  True	True	True

• Finally, using not we have

  ex1	not ex1
  False	True
  True	False

DeMorgan’s Laws Relating and, or, not

• Using ex1 and ex2 once again to represent boolean expressions, we have

  not (ex1 and ex2) == (not ex1) or (not ex2)
  

• And,

  not (ex1 or ex2) == (not ex1) and (not ex2)
  

• Also, distribution laws

  ex1 and (ex2 or ex3) == (ex1 and ex2) or (ex1 and ex3)
  ex1 or (ex2 and ex3) == (ex1 or ex2) and (ex1 or ex3)
  

• We can prove these using truth tables.

Why Do We Care?

• When we’ve written logical expressions into our programs, it no longer matters what we intended; it matters what the logic actually does.
• For complicated boolean expressions, we may need to almost prove that they are correct
• We will work through the example of writing a boolean expression to decide whether or not two rectangles with sides parallel to each other and to the x and y axes intersect.

Short-Circuited Boolean Expressions

• Python only evaluates expressions as far as needed to make a decision.

• Therefore, in boolean expression of the form

  ex1 and ex2
  

  ex2 will not be evaluated if ex1 evaluates to False. Think about why.

• Also, in boolean expression of the form

  ex1 or ex2
  

  ex2 will not be evaluated if ex1 evalues to True.

• This “short-circuiting” is common across many programming languages.

• Let’s try to check for valid input.

  x = raw_input("Enter a positive number ==> ")
  

Part 1 Exercises

1. Write a boolean expression to determine if two circles, with centers at locations x0, y0 and x1, y1 and radii r0 and r1 intersect.

2. Suppose you have a tuple that stores the semester and year a course was taken, as in

   when = ('Spring',2013)
   

   Write a function that takes two such lists as arguments and returns True if the first list represents an earlier semester and False otherwise. The possible semesters are 'Spring' and 'Fall'.

Part 2 — More Complicated/Nest If Statements

• We can place if statements inside of other if statements.

• To illustrate

  if ex1:
      if ex2:
         blockA
      elif ex3:
         blockB
  elif ex4:
      blockD
  else:
      blockE
  

• We can also work back and forth between this structure and a single level if, elif, elif, else structure.

• We will work through this example in class.

Example: Ordering Three Values

• Suppose three siblings, Dale, Erin and Sam, have heights stored in the variables hd, he and hs, respectively .
• We’d like code to print the names in order of height from greatest to least.
• We’ll consider doing this with nested if statements and with a single-level if, elif structure.

Part 2 Exercise

1. In the following code, for what values of x and y does the code print 1, for what values does the code print 2, and for what values does the code print nothing at all?

   if x>5 and y<10:
       if x<5 or y>2:
           if y>3 or z<3:
               print 1
       else:
           print 2
   

   The moral of the story is that you should be careful to ensure that your logic and if structures cover the entire range of possibilities!

2. Check that a string contains is a float.

3. Suppose we represent the date as three integers in a tuple giving the month, the day and the year, as in

   d = (2, 26, 2103)
   

   Write a Python function called is_earlier that takes two date lists and returns True if the first date, d1 is earlier than the second, d2. It should return False otherwise. Try to write this in three different ways:

   1. Nested ifs,
   2. if - elif - elif - else,
   3. A single boolean expression.

Part 3: Storing Conditionals

• Sometimes we store the result of boolean expressions in a variable for later use:

  f = float(raw_input("Enter a Fahrenheit temperature: "))
  is_below_freezing = f < 32.0
  if is_below_freezing:
      print "Brrr.  It is cold"
  

• We use this to

  • Make code clearer
  • Avoid repeating tests

Example from the Textbook

• Doctors often suggest a patient’s risk of heart disease in terms of a combination of the BMI (body mask index) and age using the following table:

  	Age	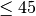Age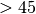
  BMI	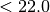Low	Medium
  BMI	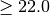Medium	High

• Assuming the values for a patient are stored in variables age and bmi, we can write the following code

  slim = bmi < 22.0
  young = age <= 45
  
  if young:
      if slim:
          risk = 'low'
      else
          risk = 'medium'
  else:
      if slim:
          risk = 'medium'
      else:
          risk = 'high'

Part 3 Exercises

1. Rewrite the previous code without the nested if’s. There are several good solutions.
2. Make the code for checking whether two circles intersect unbreakable.
3. Write code to check if two rectangles intersect.

Summary

• Logic is a crucial component of every program.
• Basic rules of logic, including DeMorgan’s laws, help us to write and understand boolean expressions.
• It sometimes requires careful, precise thinking, even at the level of a proof, to ensure logical expressions and if statement structures are correct.
  • Many bugs in supposedly-working programs are caused by conditions that the programmers did not consider.
• If statements can be structured in many ways, often nested several levels deep.
  • Nesting deeply can lead to confusing code, however.
  • Warning specifically for Python: you can easily change the meaning of your program by accidentally changing indentation. It is very hard to debug these changes.
• Using variables to store boolean values can make code easier to understand and avoids repeated tests.
• Make sure your logic and resulting expressions cover the universe of possibilities!