Relational Model and Algebra¶
Overview¶
- Relational algebra is a mathematical query language for relations.
- It is a set based query language:
- The input to each operator is one or more relations, sets of tuples.
- The output of each operator is a relation: a set of tuples.
- Relational algebra is based on a minimal set of operators that can be combined to write complex queries.
- The meaning (semantics) of other query languages, i.e. SQL, are defined in terms of relational algebra.
- SQL queries are translated to relational algebra.
- Databases implement relational algebra operators to execute SQL queries.
- Caveat: we will see a bag version of these operators for SQL later in the semester.
- Mathematical definition of database design (normalization) uses relational algebra.
Relational Algebra Overview¶
- Crucial operators (complete set):
- Union
- Set difference
- Selection
- Projection
- Cartesian Product
- Renaming
- Derived operators (added for convenience):
- Theta join
- Natural join
- Set intersection
- Each operator has a Greek symbol that starts with the same letter as the operator: Select-sigma, Project-Pi, etc.
Set operators¶
We use the term union compatible to mean that two relations have the same schema: exactly same attributes drawn from the same domain.
Given two relations R and S that are union compatible:
Union:
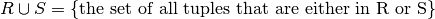
Intersection:
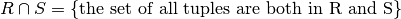
Set difference:
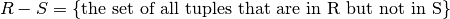
The result is a relation with same schema as R (and S).
If two relations are not union compatible, the set operation is not defined.
Note that set intersection is not technically necessary as it can driven from other operations:
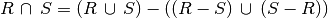
Set Operation Examples¶
The relations MarvelHeroes, DCHeroes, TVHeros are compatible, they have the same attributes.
The relations Movies and TVShows are not compatible, they have different attributes. Even if they had the same number of attributes, the name of attributes should match.
Find all heroes in the database
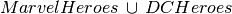
Find all heroes that are in both universes (which we know will be the empty set)
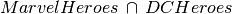
Output:
hid hero realname Find all DC comics heroes that are in a TV show

Output:
hid hero realname h8 Superman Clark Kent h9 Batman Bruce Wayne h10 Supergirl Kara Danvers h11 Flash Barry Allen h12 Arrow Oliver Queen h14 Wonder Woman Diana Prince Find all Marvel Comics heroes that are not in a TV show
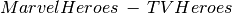
Find all heroes that are not in a TV show (both solutions are equivalent)
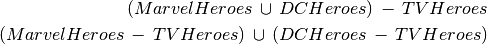
Note that set subtraction is special, it is the only way to write negation (something that is NOT true for the whole relation)
Rename¶
Rename operation renames the relation and the attributes in it. It does not change the contents of the relation.
We can use any of two following notations for rename.
Option 1.
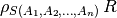
Option 2.
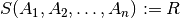
If you did not list the attributes, you are simply changing the name of the relation:
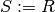
This is used to give names to intermediate results of the relational algebra operations.
Example:
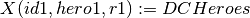
Output:
id1 hero1 r1 h8 Superman Clark Kent h9 Batman Bruce Wayne h10 Supergirl Kara Danvers h11 Flash Barry Allen h12 Arrow Oliver Queen h13 Green Lantern Hal Jordan h14 Wonder Woman Diana Prince
Selection¶
Given a relation R and a boolean condition C over the attributes of R, the selection is given by:
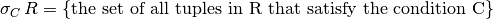
- Selection returns a new relation with the same schema as R, but containing a subset of the tuples in R based on the condition C.
All movies made before 2010
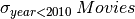
Output:
mid moviename year m2 Iron Man 2008 m4 The Incredible Hulk 2008 m13 Superman Returns 2006 m14 The Dark Knight 2008 All heroes who do not have an alias
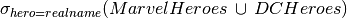
Output:
hid hero realname h15 Jessica Jones Jessica Jones All TV shows that are still running and have started after 2012.
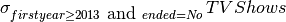
Output:
sid showname hid Channel FirstYear LastYear Ended s3 Supergirl h10 CBS 2015 2016 No s4 Gotham h9 FOX 2014 2016 No s5 Jessica Jones h15 Netflix 2015 2016 No
Projection¶
Projection does not change the tuples in the relation, but the schema of the relation.
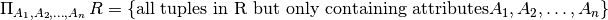
As each operator returns a set of tuples, any duplicate values will be removed. As a result, the result of a projection may contain fewer tuples than the input relation.
Find the real name of all heroes
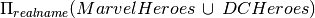
Find the id of all heroes in a TV show
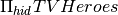
Output:
hid h3 h8 h9 h10 h11 h12 h14 h15 Find all years in which a hero movie was made
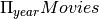
Find the id of all heroes that were both in a movie and a tv show.
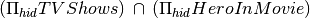
Output:
hid h12 h11 h10 h9 h15
Find the id of all movies with no heroes in them (according to our database instance)
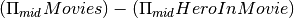
Output:
mid m10
Find start and end year of all TV shows with name The Flash.

Output:
FirstYear LastYear 2012 2016 1990 1991 Projection is crucial for changing the schema of relations, especially before a set operation!
Cartesian Product¶
Given two relations R and S that have no attributes in common,
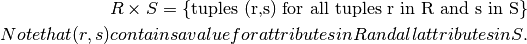
The schema of RxS is the union of the attributes in R and S. As a result, the attributes in R and S must have unique names to distinguish them from each other.
Cartesian product is a multiplication. If R has n tuples and S has m tuples, the Cartesian product will produce n*s tuples.
Cartesian product is the only way to put tuples from two relations side by side.
Cartesian Product Example¶
Given the following smaller relation instances:
HeroInMovie
| hid | mid |
|---|---|
| h1 | m1 |
| h2 | m2 |
R1(h1, hero, realname) := MarvelHeroes
| h1 | hero | realname |
|---|---|---|
| h1 | Captain America | Steve Rogers |
| h2 | Iron Man | Tony Stark |
| h3 | Hulk | Bruce Banner |
HeroInMovie x R1:
| hid | mid | h1 | hero | realname |
|---|---|---|---|---|
| h1 | m1 | h1 | Captain America | Steve Rogers |
| h1 | m1 | h2 | Iron Man | Tony Stark |
| h1 | m1 | h3 | Hulk | Bruce Banner |
| h2 | m2 | h1 | Captain America | Steve Rogers |
| h2 | m2 | h2 | Iron Man | Tony Stark |
| h2 | m2 | h3 | Hulk | Bruce Banner |
Notice that we renamed the id attribute in MarvelHeroes to make sure the schema of the two relations had no attributes in common.
If we wanted to return only the tuples with matching hero ids, we need to do a selection:
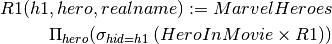
This query returns the name of all Marvel heroes who have a movie in the database.
Theta-Join (or simply Join)¶
Cartesian product is often (but not always) followed by a selection. We can define a short cut for this combination for simplicity:
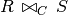
which is read as R theta join S on join condition C.
Join is the same as a Cartesian product, followed by a selection:
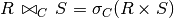
A join condition must involve expressions that compare attributes from R to S.
- Given R(A,B) and S(C,D):
- (A=C or B>D) is a join condition.
- A=5 or B=4 is not a join condition.
- Given R(A,B) and S(C,D):
We can rewrite the above query as:
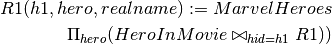
Note that you equally have to rename attributes before using theta-join to make sure join conditions can be written unambiguously.
Natural Join¶
Natural join of two relations R and S (R*S) is given by a join on the equality of all attributes in common. The common attributes are not repeated.
For example:
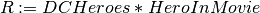
will return a relation R with schema:
R(hid, hero, realname, mid)
such that
- R matches hero ids from DCHeroes and HeroInMovie
- R only contains heroes with a movie and movies with a matching hero
- hid is not repeated
Output:
hid hero realname mid h8 Superman Clark Kent m13 h9 Batman Bruce Wayne m14 h13 Green Lantern Hal Jordan m15 h14 Wonder Woman Diana Prince m16 Find the name of all movies with the hero whose real name is Tony Stark or Bruce Wayne.
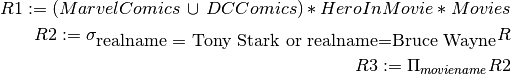
Exercises:¶
Write the following queries using relational algebra. Try the simplest possible expression possible. There may be multiple solutions to the same query.
Find the name of all movies that are released after 2014 and has a Marvel comic hero in them.
Find pairs of heroes who have starred in the same movie. Return their aliases.
Try to write this so that you only return each pair only once (do not return both a,b and b,a)
Find the name of all movies that has more than one comic hero in them.
Find the name of all movies that has more only one comic hero in them.
Find the TV shows that star heroes who have also been in a movie.
Summary¶
- Observe that there are many ways to write the same query using different relational algebra operators or different ordering of the same operators.
- Logically equivalent operations may have different time complexity, that is what query optimization is about.