Normalization¶
Overview¶
- In this topic, we will learn about a mathematical way to argue why one data model is better than the other.
- We will learn principled methods and some algorithms (i.e. decomposition) to improve a “bad” data model.
- We will talk about importance of integrity constraints in database modeling.
Why some data models can be bad?¶
Suppose we are given the following MusicGroups relation (some values fictitious):
| Group | Artist | Genre | DateFounded | DateJoined |
|---|---|---|---|---|
| Queen |
|
Pop/Rock | 1971 | 1971 |
| Queen |
|
Pop/Rock | 1971 | 1972 |
| Queen |
|
Pop/Rock | 1971 | 1971 |
| Queen |
|
Pop/Rock | 1971 | 1972 |
| Beatles |
|
Pop/Rock | 1960 | 1960 |
| Beatles |
|
Pop/Rock | 1960 | 1960 |
| Beatles |
|
Pop/Rock | 1960 | 1960 |
| Beatles |
|
Pop/Rock | 1960 | 1960 |
What is the key of this relation? Which combination of attributes must be unique for each tuple?
- Group, Artist
- Remember that you cannot have missing values for the key attributes.
What types of issues do we see with this database?
- We repeat information: Genre for a group is repeated for each
artist.
- It is possible that we make an error and change the value for one tuple. Then, we are left with not knowing what the correct genre was.
- What happens we delete all the artists in a group? We end up loosing information related to the group. Should they be coupled?
- What if a new group is formed with no artists? We had not foreseen that such a group exists. But, we cannot enter this as our data model does not allow it.
- We repeat information: Genre for a group is repeated for each
artist.
Normalization Overview¶
- Given a relation, we will examine whether all the attributes in the relation should be in the same relation or should be split into multiple relations.
- Given the meaning of these attributes, we need to write down what real
life conditions/constraints must be true.
- Can two music groups have the same name?
- Can two artists have the same name?
- Can an artist join a music group more than once?
- Often the database designer will make some assumptions regarding these.
- Having constraints will help discovery of incorrect data.
- Choose the important constraints to track.
Functional Dependency¶
A function dependency is a logical expression of the form X -> Y such that
- X, Y are sets of attributes from the database schema
- X -> Y means that whenever two tuples in a relation have the same values for attributes in X, then they must also have the same values for attributes in Y.
Functional dependencies are defined for a relation as constraints by the database designer based on the meaning of the attributes and the properties they represent
Example:
MusicGroups(name, artist, genre, dateFounded, dateJoined) name -> genre dateFounded name artist -> dateJoined
name -> genre dateFounded
Means that given group name, there is a single genre and a single value for the dateFounded attribute
name artist -> dateJoined
Means that given a group name and an artist, there is a single dateJoined corresponding to the date the artist joined the group.
What if an artist joins the group multiple times? According to our data model, we are not going to store that. Remember, you define the rules for your database.
Example
People(Name, Phone, InsCompName, InsCompAddress) Name -> Phone, InsCompName InsCompName -> InsCompAddress
Example
Companies(company_name, company_address, date_founded, owner_id, owner_name, owner_title, #shares) company_name -> company_address company_name -> date_founded company_name, owner_id -> owner_title company_name, owner_id -> #shares company_name, owner_title -> owner_id owner_id -> owner_name
- Rules of this database according to these functional dependencies:
A single owner can only hold any specific title
company_name, owner_title -> owner_id
An owner can have a single title within the company
company_name, owner_id -> owner_title
Each title is given to a single person within the company
company_name, owner_title -> owner_id
Keys and functional dependencies¶
Functional dependencies tell us what the keys are!
For example
Student(id, name, address) id -> name, address (FD1)
means that all tuples with the same id must have a unique name and address.
Then id is the key! No two tuples can have the same id, but different name or address. So, id must be unique.
But if the above is true, then we must also have that:
id name -> name, address (FD2)
Then, id, name is a key too. Which one is better? The smaller one!
Also, the functional dependency FD1 is stronger than FD2, i.e. you can obtain FD2 from FD1.
Functional Dependencies¶
- For a given relation, we look at all valid set of functional dependencies together.
- We will use F to denote the set of all functional dependencies.
- All functional dependencies in F together tell us all the relevant rules for our relation, such as the type of tuples can we store.
- Given F, we can also infer new rules using the following inference rules.
- Some functional dependencies may be removed if they are not needed and some may be simplified based on others. To do this, we will see some rules first.
Superkey: Unique Attributes¶
Given a relation R(A1,…,An) and a set of functional dependencies F, a superkey (superset of keys) is a set of attributes B1,…,Bm such that
B1,…,Bm imply all the attributes in relation R. This is called uniqueness constraint.
No two tuples may have the same values for the attributes B1,…,Bm.
In other words,
- ::
Given F:
B1,…,Bm -> A1,…,An
is implied by the functional dependencies in F.
Keys¶
- Given a relation R(A1,…,An) and a set of functional dependencies F,
a key is a set of attributes B1,…,Bm such that
- B1,…,Bm is a superkey! This is called the uniqueness constraint.
- No subset of B1,…,Bm is a superkey. This is called the minimality constraint.
- From now on we will use X, Y to represent a set of attributes.
Functional Dependency Inference¶
The rules below allow us to find whether a functional dependency is implied the others?
If you apply all the rules in any order from a given set F and obtain the functional dependency X->Y, then X->Y is implied by F.
A shortcut: compute the closure of X+ with respect to F.
If Y⊆X+ with respect to F then X->Y is implied by F.
The algorithm is below.
Functional Dependency Inference Rules¶
Trivial Functional Dependencies (Reflexivity)
If Y ⊆ X, then X ->Y is true for all relations.
Proof. If two tuples have the same values for attributes in X, then it is already given that they have the same values for the attributes of Y.
Splitting Rule
Given a functional dependency A1,...,An -> B1,...,Bm we can split it into singletons on the right hand side: A1,...,An -> B1 .... .... A1,...,An -> Bm
Combining Rule
Given functional dependencies A1,...,An -> B1 .... .... A1,...,An -> Bm we can combine the attributes on the right hand side: A1,...,An -> B1,...,Bm
Transitivity
Given functional dependencies X -> Y and Y -> Z we can conclude that: X -> Z
for sets of attributes X, Y and Z.
Augmentation
If A1,...,An -> B1,...,Bm and given attributes C1,...,Ck we can conclude that A1,...,An,C1,...,Ck -> B1,...,Bm,C1,...,Ck
Note that reflexivity, augmentation and transitivity are sufficient and necessary rules. The rest of the rules can be driven from these three.
Inference example using the above rules¶
Given: F = {A -> BC, CD -> F, BE -> D} for R(A,B,C,D,E,F) Is AE -> CDF true?Apply all the inference rules to get this:
BE -> D (given) BCE -> CD (accumulation of BE -> D) BCE -> D (decomposition) A -> BC (given) AE -> BCE (acculumulation) AE -> D (transitivity) AE -> BCDE (combining rule) AE -> CD (decomposition) AE -> F (transitivity) AE -> CDF (combining rule)
- Method 2: compute the closure of AE to find all that is implied by AE. See method below.
Closure of a set of attributes¶
Given a relation R and a set of functional dependencies F, we need a way to find whether a functional dependency X -> Y is true with respect to F.
Given a set F of functional dependencies, the closure X+ of a set X of attributes is given by the following algorithm.
- Initialize, X+ = X
- Find any functional dependency Y -> Z in F such that Y ⊆ X+, then X+ = X+ ∪ Z.
- Continue until X+ does not change.
Inference rule:
If Y⊆X+ with respect to F then X->Y is implied by F.
Closure Example¶
Given A -> BC, CD -> E, BE -> C
AE closure must include AE (given AE, we know AE).
Now given we know AE, what else can we conclude based on the above fds?
AE + = {AE}, use A -> BC to get:
AE + = {ABCE} nothing else we can use. So, we are finished.
This means: AE -> ABCE.
We can also write it as:
AE -> A, AE -> B, AE->C, AE->E
Keys revisited¶
A key for a relation R is a minimal set of attributes A1,..,An such that {A1,…,An}+ is the set of all attributes in R.
Given:
name -> genre dateFounded
name artist -> dateJoined
key: name artist
{name artist}+ = {name, artist, genre, dateFounded, dateJoined}
Find the keys for the following relations:
R1(A,B,C,D,E,F,G) F = {A->BC, AD->EF, AC->G} R2(A,B,C,D,E) F = {A->BC, D->E} R3(A,B,C,D) F = {A->BC} R4(A,B,C,D,E,F,G) F = {A->BCD, BE->FG, CG->A}
Simplifying the set of functional dependencies¶
- Given a key for a relation, we would like to argue whether the underlying model is a good model or not (using normal forms).
- To accomplish this, we need to first start with a minimal set of functional dependencies, those that cannot be simplified. Let’s define this first using the notion of a closure of all functional dependencies.
Closure of a set of functional dependencies¶
Closure F+ of a set F of function dependencies is the set of all functional dependencies that can be inferred by the given set of inference rules.
Closure F+ includes all dependencies in F.
F ⊆ F+
Closure includes all trivial functional dependencies.
Closure also includes all other non-trivial dependencies that can be inferred by using the above rules.
Two sets of functional dependencies F1 and F2 over the same relation are equivalent, if they have the same closure:
F1 equivalent F2 iff F1+ = F2+
Basis of Functional Dependencies¶
Basis: A basis is a set of functional dependencies such that there is only one attribute on the right hand side of a functional dependency.
It is easy to convert any functional dependency set to a basis by using the splitting rule.
F = {A->BC, CD->EF}
convert to:
F = {A->B, A->C, CD->E, CD->F}
Remember, split the right hand side. The left hand side should not be changed unless it is implied by other functional dependencies as we will see next.
Minimal Set of Functional Dependencies¶
A basis F is minimal if there is no other basis F1 that can be obtained from F by
- either removing some functional dependencies
- or by removing some attributes from the left hand side of functional dependencies
such that F and F1 are equivalent (i.e. they have the same closure).
Finding a minimal basis¶
Input a basis F.
Step 1.
For each fd X -> Y in the set F, check if F - { X -> Y } implies X -> Y. If so, remove X -> Y.
Step 2.
For each fd XW -> Y in the set F, check if X+ is the same with respect F and (F - { XW -> Y }) ∪ { X -> Y }.
Example¶
F = {ABC -> D, AB -> E, E -> C, ABE -> C, E -> F, A -> A}
Step 1. Can we remove ABE -> C ?
Given F, ABE+ = {A,B,C,D,E,F}
Given F1 = {ABC -> D, AB -> E, E -> C, E -> F},
ABE+ = {A,B,C,D,E,F}.
As they are equivalent, we can remove ABE -> C.
We can also remove any functional dependency that is trivial, i.e. A -> A.
F = {ABC -> D, AB -> E, E -> C, E -> F}
Step 2. Can we replace ABC ->D with AB -> D ?
Given F:
AB+ = {A,B,C,D,E,F}
Given F2={AB -> D, AB -> E, E -> C, E -> F}:
AB+ = {A,B,C,D,E,F}.
As they are equivalent, we can replace with F with F2.
Normalization¶
Given a schema, are there any problems with the way the attributes are grouped into the relations?
Example:
Person(Name, Phone, InsCompName, InsCompAddress)
When two people have the same insurance company (InsCompName), then the insurance company address of these two people should also be the same.
- Possible problems:
- If we insert a new person with the same insurance company but different address, the database becomes inconsistent. Addition of an atomic unit of information should not cause inconsistency.
- If we delete a person with a specific insurance company X and if there are no other people with this insurance company, we loose the information about where this company is located.
- If we update the insurance information for one person but not the others with the same insurance, then the database becomes inconsistent -similar to insertion above.
- Possible problems:
Normal Forms¶
- Normal forms are introduced as rules that help avoid the above problems, based on the functional dependencies true for this relation.
- We have already seen first normal form: all attributes should have simple values.
Boyce-Codd Normal Form (BCNF)¶
- Given a set F of functional dependencies, a set R is said to be in
Boyce-Codd normal form if all functional dependencies X -> Y in F
are
- either trivial, i.e. Y ⊆ X
- or has a superkey on the left side (i.e. X is a superkey).
BCNF¶
Example:
Person(Name, Phone, InsCompName, InsCompAddress) Name -> Phone, InsCompName InsCompName -> InsCompAddress Key: Name
Not in BCNF since the second f.d. does not have a superkey on the left (InsCompName is not a superkey).
Example:
MusicGroup(name, artist, genre, dateFounded, dateJoined) name -> genre dateFounded name artist -> dateJoined Key: name, artist
Not in BCNF since the first f.d. violates it (name is not a superkey)
Example:
BankAccount(routingno, accountno, userid, bankname, bankaddress) userid, routingno, accountno -> bankname, bankaddress userid, bankname, accountno -> routingno Key: userid, routingno, accountno or userid, bankname, accountno
In BCNF because both keys have a superkey on the left hand side.
Example:
Student(Id, lastname, firstname, SSN, firstmajor, year, email) id -> lastname firstname ssn firstmajor year email ssn -> id lastname firstname firstmajor year email email -> lastname firstname id ssn firstmajor year Key: id or ssn or email
In BCNF because all functional dependencies have a superkey on the left.
Prime attribute¶
- Given a relation R and a set of functional dependencies, a prime attribute is an attribute that appears in a key for R.
Third Normal Form (3NF)¶
Given a set F of functional dependencies, a set R is said to be in third normal form if all functional dependencies X -> Y in F are
- either trivial, i.e. Y ⊆ X,
- or has a superkey on the left side (i.e. X is a superkey),
- or has only prime attributes on the right hand side (i.e. all attributes in Y are prime attributes).
Example:
Address(city, state, street, zip) city, state, street -> zip zip -> city, state Key: city, state, street or zip, street Prime attributes: city, street, state, zip
This is not in BCNF because the second functional dependency does not have a superkey on the left. However, as city and state are both prime attributes, this relation is in 3NF.
- First functional dependency is not trivial but has a superkey on the left.
- The second functional dependency is not trivial, does not have a superkey on the left, but all attributes on the right are prime attributes.
BCNF and 3NF relations¶
- All relations that are in BCNF are also in 3NF. The reverse is not true.
- In the above example, Address is in 3NF but not in BCNF.
- BCNF is the golden standard, it is desirable to put all relations in BCNF.
- If a relation is not in BCNF, we need to decompose the it to get relations
that are in BCNF.
- There is no single way to do this. You need to run the algorithm multiple ways and choose the most reasonable solution.
- If a relation is not in 3NF, there is a simple algorithm to
decompose it into relations that are in 3NF.
- It will produce a single result.
- We will now see how to do decompositions!
Decomposition¶
For example, we know that the following relation is not in BCNF:
Person(Name, Phone, InsCompName, InsCompAddress)
Because insurance information belongs in a different relation than people. A better model would be:
Person(Name, Phone, InsCompName), Insurance(InsCompName, InsCompAddress)
This act of splitting the relation is called decomposition.
The objective is to have relations that are atomic, contain only information relevant to the key as a whole, have fever null values.
Given a relation R and functional dependencies F, a decomposition is given by
R1(A1,..,An), F1 R2(B1,...,Bm), F2
such that
Atttributes in R1 and R2 together are equivalent to attributes in R
F1 only involves attributes in R1, and F1 ⊆ F+
F2 only involves attributes in R2, and F2 ⊆ F+
Tuples in R1 and R2 are obtained from R:
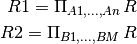
Decomposition Properties¶
Suppose we are given a decomposition
R1(A1,..,An), F1 and R2(B1,…,Bm), F2
of a relation R with functional dependencies F.
The decomposition is dependency preserving iff
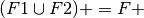
The decomposition is lossless if we are guaranteed that
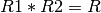
The natural join of tuples is guaranteed to return the same relation as R.
We will now see how to create decompositions that satisfy these conditions.
Projecting functional dependencies¶
The functional dependencies for a decomposition are found by projecting the original set F of functional dependencies on the decomposed relation.
Given:
R(A,B,C), F = {A -> B, B -> C} Decompose into: R1(A,B) and R2(A,C)
What are the maximal set of functional dependencies implied by original set, but only involve attributes in R1 or R2?
First find all (non-trivial) functional dependencies implied by the above:
A -> B, B -> C, A -> C, AB -> C, etc.
Now, for R1(A,B): choose the subset of these that have only A and B (A -> B)
For R2(A,C): choose the subset that have only A and C (A -> C)
Simplify each set to be a minimal basis!
Is this decomposition after choosing best functional dependencies preserve them all?
In other words, did we loose something by decomposing:
R(A,B,C), F = {A -> B, B -> C} into: R1(A,B) F1 = {A -> B} R2(A,C) F2 = {A -> C}
We check if this decomposition is dependency preserving.
F1 ⋃ F2 and F are equivalent F1 ⋃ F2 = {A -> B, B -> C} F = {A -> B, A -> C }Are the two equivalent?
F1: A -> B, B -> C
F1 implies everything in F2
F2: A -> B, A -> C
F2 does not imply everything in F1 (i.e. B -> C)
B+ = {B}, does not include C.
Hence, F1 and F2 are not equivalent. Actually, F1 is more strict than F2.
This means that this decomposition is not dependency preserving as B -> C is lost!
Given: R(A,B,C), A -> B, B -> C
Suppose we decompose R into R1(A,B) and R2(A,C)
Can we still enforce the above functional dependencies?
Projecting functional dependencies (Algorithm)¶
- Suppose we are given a set of functional dependencies F for a relation R. We decompose the relation to a subset of the attributes L, R1 = ΠL R.
- The functional dependencies that hold for R1 are computed as follows:
- For all possible subsets X of L, compute X+ with respect to F.
- For all attributes A in X+ that are in L, add the dependency X -> A to the projection.
- Simplify the basis to find a minimal basis.
Dependency Preserving¶
Given a set F of functional dependencies for R, a decomposition R into R1, R2 is dependency preserving if
Let F1 be the projection of F onto R1
Let F2 be the projection of F onto R2
If F1 ∪ F2 ≡ F then the decomposition is dependency preserving.
This is the same as checking: (F1 ∪ F2)+ = F+
Chase test for lossless decomposition¶
- The chase test for lossless decomposition works as follows:
- Given a decomposition R1,…,Rn we construct a relation R with a tuple for each decomposition. For each attribute, we will use a symbol (usually a lowercase letter).
- The tuple for relation Ri has the specific symbol for each attribute in the relation. But, the symbols for the attributes in Ri have no subscript. The remaining symbols have subscript i.
- Given a functional dependency X -> Y, we find two tuples t1, t2 such
that the attributes in X are the same for these tuples. Then, we set
attributes in Y for these two tuples to be the same as follows:
- If the attributes have both subscript, then set one to be equivalent to the other arbitrarily.
- If one of the attributes have no subscript, then change the other so that it has no subscript as well.
- We continue to apply the functional dependencies until we find a tuple with no subscripts, which is a proof that the decomposition is lossless, and stop.
Chase Algorithm Examples¶
Example:
Given R(A,B,C) and F = {C -> B} Decompositions R1(A,C) and R2(B,C)
We have following starting relation:
| A | B | C |
|---|---|---|
| a | b1 | c |
| a2 | b | c |
- Apply C->B to get:
| A | B | C |
|---|---|---|
| a | b | c |
| a2 | b | c |
This is the point we stop. This decomposition is losless as the first tuple is without a subscript.
Example:
R(A,B,C,D,E,F) F= {B->E, EF->C, BC->A, AD->E} R1(A,B,C,F) R2(A,D,E) R3(B,D,F)
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| a | b | c | d1 | e1 | f |
| a | b2 | c2 | d | e | f2 |
| a3 | b | c3 | d | e3 | f |
- Apply B->E to rows 1 and 3.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| a | b | c | d1 | e1 | f |
| a | b2 | c2 | d | e | f2 |
| a3 | b | c3 | d | e1 | f |
- Apply EF->C to rows 1 and 3.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| a | b | c | d1 | e1 | f |
| a | b2 | c2 | d | e | f2 |
| a3 | b | c | d | e1 | f |
- Apply BC->A to rows 1 and 3.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| a | b | c | d1 | e1 | f |
| a | b2 | c2 | d | e | f2 |
| a | b | c | d | e1 | f |
- Apply AD->E to rows 2 and 3.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| a | b | c | d1 | e1 | f |
| a | b2 | c2 | d | e | f2 |
| a | b | c | d | e | f |
The last row has no subscripted letters, hence this is a lossless decomposition.
Example:
- ::
R(A,B,C) {A->C} R1(A,B) R2(B,C)
| A | B | C |
|---|---|---|
| a | b | c1 |
| a2 | b | c |
Cannot apply any functional dependencies and this relation is a lossy.
We can use the above relation as proof of this:
R1:
| A | B |
|---|---|
| a | b |
| a2 | b |
R2:
| B | C |
|---|---|
| b | c1 |
| b | c |
R1*R2 (natural join) results in a different relation than R:
| A | B | C |
|---|---|---|
| a | b | c1 |
| a | b | c |
| a2 | b | c |
| a2 | b | c1 |
Objectives for Decomposition Methods¶
If we are decomposing relations to obtain BCNF or 3NF relations:
All our decompositions must be lossless
It is highly desirable that decompositions are dependency preserving, but that may not always be possible.
In this case, choose the least important dependencies to let go.
Decomposition into BCNF¶
Given a set of functional dependencies F for a relation R(A1,…,An) that violate BCNF,
- Convert F to minimal basis
- Find a functional dependency X -> Y that violate BCNF
- Compute X+
- Decompose R into two: a relation R1 containing attributes in X+ and a relation containing attributes {A1,…,An} - (X+ - {X}).
- Find projection of f.d.s into R1 and R2, now recursively apply BCNF decomposition to R1 and R2 (with corresponding set of functional dependencies) until all the relations are in BCNF.
Example
MusicGroup(name, artist, genre, dateFounded, dateJoined) name -> genre dateFounded name artist -> dateJoined Key: name, artist Given name -> genre dateFounded violates BCNF, decompose into: R1(name, genre, dateFounded), name -> genre dateFounded R2(name, artist, dateJoined), name artist -> dateJoined
Notes about BCNF Decomposition¶
BCNF decomposition algorithm is non-deterministic. Depending on the choice of functional dependency you choose in each step, you may get a different output.
You must use judgment of which decomposition results in a better data model.
While BCNF decomposition is lossless, it is not always guaranteed to be dependency preserving.
Also, sometimes BCNF may result in unintuitive results.
Example:
tracks(album, trackNo, song, version) album trackNo -> song song version album -> trackNo Key: song, version, album or album, trackNo, version Not in BCNF due to album trackNo -> song
BCNF Decomposition requires us to create relations:
tracks1(album, trackNo, song) album trackNo -> song tracks2(song, version)
This decomposition is not desirable for two reasons:
- The second dependency is lost: there is no way now to check for it after decomposition.
- These four attributes semantically belong together, but BCNF decomposition is forcing us to divide them into different relations.
3NF decomposition algorithm¶
- Given a set F of functional dependencies that form a minimal basis
for a relation R, use the combining rule for F to combine all f.d.s
with the same left hand side. (this is an optional step as discussed
in the example below)
- Decomp = {}
- For each functional dependency X -> Y in F:
- If there is no relation in Decomp that contains all the attributes in X and Y then add a relation with attributes X∪Y to Decomp.
- If there are no relations in Decomp that have all the attributes of one of the keys of R then, add a new relation to Decomp that contain all the attributes in one of the keys of R.
- Simplify Decomp: If R1,R2 are in Decomp but R2 contains all the attributes in R1 then remove R1.
- The algorithm guarantees that
- the resulting relations are in 3NF,
- the decomposition is dependency preserving, and
- the decomposition is lossless
3NF Decomposition Examples¶
Given
R(A,B,C,D,E,F) F = {AB -> C, AB -> F, C -> A, BC -> D} Key: ABE or BCE (not in 3NF or BCNF)
Before decomposing, join the right hand sides for F to get:
F = {AB -> CF, C -> A, BC -> D} R1(A,B,C,F) {AB -> CF, C -> A} Key: AB R2(B,C,D) {BC -> D} Key: BC R3(A,B,E) Key: ABE
Note: no need to create a new relation for C -> A if we already created R1. If R1 is created afterwards, we will remove the relation with attributes (A,C) in the simplification step.
Note: R3 is needed as no relation has all the attributes of a key (either ABE or BCE is enough)
Note: What happens if we do not use the combining rule? We would get the following decomposition:
R1(A,B,C) {AB -> C, C->A} R2(A,B,F) {AB -> F} R3(B,C,D) {BC -> D} R4(A,B,E)
Attributes A,B,C,F are now distributed to two relations. This may be desirable in some applications, allowing us to separate frequently queried attributes from the other. However, it may also be very undesirable if we need to join R1 and R2 all the time. It will really depend on the use of these relations.
Fourth Normal Form (4NF)¶
Suppose we have
People(id, hobby, phone)
As hobby and phone can take multiple values, there are no functional dependencies for this relation. So, it is in BCNF.
But, there is still a problem:
Hobby and phone take multiple values but they are not related. Why put them in the same relation?
We must separate them.
Decompose into
PersonHobby(id, hobby) PersonPhone(id, phone)
Multivalued dependencies shows the technical way to accomplish this.
Multi-valued dependencies¶
A multi-valued dependency of the form
A1 ... An =>> B1 ... Bm
means that for all pairs of tuples t1 and t2 that agree on A, we can find a tuple v in R such that
- v agrees with t1 and t2 on As
- v agrees with t1 on B’s
- v agrees with t2 on the remaining attributes (not As or Bs)
For example, suppose we have that
hero(name, weaponsused, hobby) name =>> hobby
This means that we would expect to see tuples as follows:
| hero | weaponsused | hobby | tuple |
|---|---|---|---|
| lara | ice axe | relic collecting | t1 |
| lara | compound bow | motorcycling | t2 |
| lara | ice axe | motorcycling | |
| lara | compound bow | relic collecting | v |
where for t1 and t2 given as above, we need to have v that agrees with the hobby for t1 and weaponsused for t2.
In other words, unless we store all possible combination of values for Bs and the remaining attributes, we claim that there is a relation between them. But, the multi-valued functional dependency
A1 ... An =>> B1 ... Bm
claims that Bs and the remaining attributes are unrelated.
Inference rules¶
- Trivial MDs, A1 … An =>> B1 … Bm is true if {B1, …,Bm } ⊆ {A1,…,An}
- The transitive rule: X =>> Y and Y =>> Z implies X =>> Z (where X,Y,Z are sets of attributes).
- If A1 … An -> B1 … Bm then A1 … An =>> B1 … Bm is also true.
- A1 … An =>> B1 … Bm is true and C1 … Ck are all the attributes in R that are not As or Bs then A1 … An =>> C1 … Ck is also true.
- Note that the splitting/combining rule does not apply to MVDs.
Fourth Normal Form¶
- A relation is fourth normal form iff whenever A1 … An =>> B1 … Bm is a non-trivial MVD, then A1 … An is a superkey.
- To decompose a relation into Fourth normal form, use an algorithm similar to BCNF decomposition algorithm using MVDs.
- Relations in 4NF ⊆ Relations in BCNF ⊆ Relations in 3NF.
4NF decomposition¶
Given a relation R where A1 … An =>> B1 … Bm violates the 4NF, decompose R into:
R1(A1,…,An,B1,..,Bm)
R2 contains all attributes except for B1,…,Bm.
If the resulting relations are not in 4NF, then continue decomposing until they are.
Summary¶
Make sure that all tables in your database are in 3NF and 4NF in the least, and BCNF if possible.
All decompositions you perform should be lossless.
Not all decompositions can be necessarily dependency preserving.
Choose which dependencies are important to enforce for your application and find ways to enforce them, either through integrity constraints or other application logic.
Normalization and decomposition is one way of thinking of improving a data model, but may not necessily help design the database from scratch.
- It does not help when you have already normalized the database too far, splitting related information across different tables.
- It does not help you see the big picture.
We will learn E-R modeling methodology to design a full database, but with normalization in our minds.