CSCI 4972/6963 - Spring 2007
Advanced Computer Graphics

Home
Contact Information
Office Hours

Syllabus
Prerequisites
Textbook

Grading
Assigned Readings

Calendar
  Lecture notes
  Lab materials
  Homework
  Test reviews

Homework
  Collaboration Policy
  Compilers
  Homework Late Policy
  Electronic Submission

Assignment 1: Transformations & OpenGL Warmup

The goal of this assignment is to get comfortable with the programming environment you will be using for this class, familiarize yourself with two simple libraries that we will use for linear algebra and images. It's an opportunity for a crash course in C++ and OpenGL (if you're not already familiar with them). Here are a couple tutorials you may want to check out:

The incidental goal is also to have fun with bizarre fractal objects. IFS are self-similar fractals: a subpart of the object is similar to the whole. The classic example of an IFS is Barnsley's fern, where each subpart of the fern is exactly the same as the whole fern. IFS are described by a set of affine transformations (rotations, translations, scale, skew, etc.) These transformations capture the self-similarity of the object. IFS can be defined in any dimension, and we will play with both two-dimensional and three-dimensional ones. Formally, an IFS is defined by n affine transformations. Each transformation f_i must be contractive: The distance between points must be reduced. An attractor of the IFS is the object such that A = U f_i (A). A is unchanged by the set of transformations: It is a fixed point.

We can render an IFS by iterating the transform on random input points from the unit square. We approximate the fixed point by applying the transformation many times. The algorithm is as follows:

   for "lots" of random points (x₀, y₀)
       for k=0 to num_iters
           pick a random transform f_i
           (x_k+1, y_k+1) = f_i(x_k, y_k)
       display a dot at (x_k, y_k)

To reduce the number of points necessary to make an image of reasonable quality, probabilities are assigned to each transformation, instead of choosing a transformation with uniform probability.

Tasks

Download the provided source code and set up your C++ development environment. To receive full credit, your code must compile and run without errors using gcc 3.4.x. Even if you plan to do much of your development in another environment, you'll probably still want to set up gcc so that you can test it before submission. A Makefile is provided for use with either Unix or Cygwin.
For interactive display of your IFS, you will use the OpenGL API that uses graphics hardware for fast rendering of 3D primitives. Note: with some configurations, software emulation might be used, resulting in slower rendering. If the machine you're working on does not have OpenGL and GLUT, you will need to download these libraries yourself from http://www.opengl.org. Adjust the CC, INCLUDE_PATH, and LIB_PATH lines of the Makefile as necessary for your installation.
All files implementing OpenGL code should include the OpenGL header files:
```
   // Included files for OpenGL Rendering
   #include <GL/gl.h>
   #include <GL/glu.h>
   #include <GL/glut.h>
```
When provided with appropriate arguments, the initial executable should launch an OpenGL window and draw a cube and you should be able to navigate the scene with the mouse (left button rotates, middle button translates, right button zooms). Try this at the command prompt:
```
ifs -gui -size 500
```
Now you're ready to start coding. Write a C++ class IFS that renders iterated function systems, including the interface (in a file ifs.h) and the implementation (ifs.C). The IFS class should include:
- a field to store n, the number of transformations,
- an array of matrices representing the n transformations,
- an array of the corresponding probabilities for choosing a transformation,
- a constructor that parses the input file and creates an IFS,
- a render method that creates and saves and image of the IFS,
- a paint method which makes appropriate OpenGL calls to draw points or polygons to the OpenGL window, and
- a destructor that frees the memory of the various arrays (using delete).
When you're done, adjust the main function (provided in main.C) if necessary so your program creates an Image instance, reads an IFS description from a file, and (depending on the command line arguments) either renders and saves the IFS to the image or launches the OpenGL window as appropriate.
Use the linear algebra library for the point and transformation representations.
Perform proper memory management --- free memory when an object is destroyed. In high-performance graphics applications careful management of resources is essential!
In your README.txt comment on the performance of your programming environment. How many polygons/points can you render interactively? What improvements could you make to your code?

Extensions

Implement at least one additional feature in your program. Examples include:

design a new IFS --- figure out the transformations and probabilities,
automatically determine the bounding box of the fractal object,
change the color scheme,
implement anti-aliasing,
experiment with depth-first vs. breadth-first, etc.

Include a short paragraph in your README.txt file describing your extension(s).

Hints

Random numbers can be obtained using the drand48() or rand() and RAND_MAX. See stdlib.h.
To debug your code, set the number of iterations to one. This will allow you to check that you got the transformations right.
Be careful, arrays are indexed from 0 to n-1 in C++. Reading beyond the bounds of the array will probably result in a segmentation fault.
Use assert() to check function pre-conditions, array indices, etc. See assert.h.
To perform transformations in OpenGL, read about the Modelview matrix stack and the OpenGL commands glMatrixMode(), glPushMatrix(), glPopMatrix(), and glMultMatrix() in the OpenGL Programming Guide, Chapter 3.

Provided Files (files.zip)

Image Library (image.h & image.cpp)
The Image class is used to initialize and edit the rgb values of images. Be careful --- do not try to edit values outside the bounds of the image. The class also includes functions for loading and saving simple uncompressed .tga image files. The .tga image files can be viewed with xv or opened in Photoshop and other image viewers/editors. The unix command line program mogrify is useful for converting between different image representations.
Linear Algebra Library (vectors.h & matrix.h & matrix.cpp)
Linear algebra support for floating point vectors with 2, 3, and 4 elements (Vec2f, Vec3f, and Vec4f) and 4x4 floating point matrices (Matrix). For this assignment, the void Matrix::Transform(Vec3f &v) function will be handy.
Parsing code for command-line arguments and input files (argparser.h & parse.cpp)
Your program should take a number of command line arguments to specify the input file (-input), number of points (-points), number of iterations (-iters), output size (-size), and whether to render to an output image file (-output), or launch the OpenGL window (-gui). If the gui is selected, draw points by default, or cubes if -cubes is specified. Make sure all of the examples below work, as this is how we will test your program. Code to parse input files and command line arguments is provided:
OpenGL and main code (main.cpp, ifs.h, glCanvas.h, glCanvas.cpp, camera.h, camera.cpp)
OpenGL programs can be tricky to set up from scratch. This base code should do all that work for you.
Makefile for g++ on UNIX or Windows/Cygwin
On the command line simply type make unix (or make cygwin_x or make cygwin). To force a re-build of all object files, type make clean first.
Data files (fern.txt, dragon.txt, sierpinski_triangle.txt, and giant_x.txt)
The input data for an IFS is a file which contains n, the number of transforms, followed by the probability of choosing each transform and a 4x4 floating point matrix representation of the transform.

Sample Results

ifs -input sierpinski_triangle.txt -points 10000 -iters 0 -size 200 -output sierpinski_triangle_0.tga
ifs -input sierpinski_triangle.txt -points 10000 -iters 1 -size 200 -output sierpinski_triangle_1.tga
ifs -input sierpinski_triangle.txt -points 10000 -iters 2 -size 200 -output sierpinski_triangle_2.tga
ifs -input sierpinski_triangle.txt -points 10000 -iters 3 -size 200 -output sierpinski_triangle_3.tga
ifs -input sierpinski_triangle.txt -points 10000 -iters 4 -size 200 -output sierpinski_triangle_4.tga
ifs -input sierpinski_triangle.txt -points 10000 -iters 30 -size 200 -output sierpinski_triangle.tga

ifs -input fern.txt -points 50000 -iters 30 -size 400 -output fern.tga

ifs -input giant_x.txt -points 10000 -size 400 -gui -iters 0
ifs -input giant_x.txt -points 10000 -size 400 -gui -iters 1
ifs -input giant_x.txt -points 10000 -size 400 -gui -iters 2
ifs -input giant_x.txt -points 10000 -size 400 -gui -iters 3
ifs -input giant_x.txt -points 10000 -size 400 -gui -iters 4

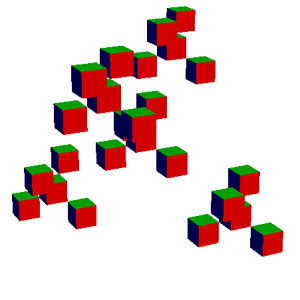
ifs -input giant_x.txt -size 400 -gui -iters 0 -cubes
ifs -input giant_x.txt -size 400 -gui -iters 1 -cubes
ifs -input giant_x.txt -size 400 -gui -iters 2 -cubes
ifs -input giant_x.txt -size 400 -gui -iters 3 -cubes
ifs -input giant_x.txt -size 400 -gui -iters 4 -cubes

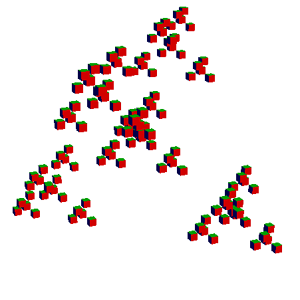
Please read the Homework information page again before submitting.