Transaction Management - Concurrency¶
Overview¶
Transaction management is about making sure that when database operations change data, they do not cause problems.
Problems may occur because:
- Concurrency: multiple transactions may need to read or write the same data as well as transactions aborting due to different reasons
- Unforeseen problems: Software or hardware crashes, especially problematic is loss of state: loss of all data currently in memory
We want to ensure some basic guarantees:
- Atomicity: All or nothing. Transactions cannot half-complete, either they finish all operations or make no changes
- Consistency: Transactions must execute the operations correctly (assuming that they are correctly written pieces of code)
- Isolation: Transactions are written as if they are the only program executing in the database (in isolation from any other program). Their effects should reflect that.
- Duration: Once a transaction is successfully completed, its effects should be recorded on disk and never be lost.
In this lecture, we will concentrate on the “isolation” component assuming atomicity and consistency are ensured.
Making sure isolation is satisfied means that concurrent transactions cannot erase each others data.
Abstracting Transactions¶
To study concurrency, we will abstract how we view transactions.
The only operations that matter in a transaction are the data items the transaction reads or writes.
T1: r1(X), r1(Y), w1(Y), commit1 T2: r2(X), w2(X), r2(Z), w2(Z), commit2
This transaction reads two data items and writes only one.
Multiple transactions may execute concurrently and their operations may interleave.
The sequence of operations that take place in the DMBS is called a schedule.
S1: r1(X), r2(X), r1(Y), w2(X)
- This schedule shows a partial execution of T1 and T2.
- Unless we see a commit or abort, we assume that T1 or T2 are not yet finished.
- The ordering of the operations is likely determined by many things: which operation gets executed first and which operation is delayed due to concurrency control.
Serial Schedules¶
- Given each transaction is supposed to be a correct piece of code if executed completely, then any ordering of transactions is acceptable.
- A serial schedule is one in which one transaction executes at a time.
- Any serial schedule is an acceptable schedule.
- Any schedule that is guaranteed to produce the same result as a serial schedule is an acceptable schedule.
- How do we know two schedules have the same result?
Schedule Equivalence¶
Two schedules are guaranteed to have same results if they will read the same values and write the values in the same order.
For example:
S1: r1(X) r2(X) r2(Y) w1(X) w2(Y) S2: r2(X) r2(Y) w2(Y) r1(X) w1(X) S3: r1(X) w1(X) r2(X) r2(Y) w2(Y)
S1 and S2 are equivalent: T2 reads X before T1 writes it.
S1 and S3 are not necessarily the same. In S3, T2 reads X after T1 writes, so the value read may be different.
Conflict Ordering¶
A conflict is given by a pair of operations
op1_i(X) ... op2_j(X)
on the same item (e.g. X) by two different transactions (e.g. i and j) and at least one of the operations is a Write.
Basically, all potential conflict examples are:
r1(X) ... w2(X) w1(X) ... r2(X) w1(X) ... w2(X)
In each case, if two schedules switch the ordering of any of these operations, the result will not be the same.
Examples:
S1: r1(X) ... w2(X) S2: w2(X) ... r1(X)
In this case, the value read by r1 may be different.
S1: w1(X) ... w2(X) S2: w2(X) ... w1(X)
In this case, the last value written is changed and may not be the same.
Serializable schedules¶
If two schedules S1 and S2 have the same ordering for all conflicting operations, then they will have the same result.
Such schedules are called conflict equivalent.
Conflict equivalent schedules will always have the same result.
If a schedule S1 is (conflict) equivalent to a serial schedule S, then we say that S1 is serializable.
Algorithm to check serializability¶
To find whether a given schedule is serializable, we need to draw the conflict graph.
Each transaction in the schedule is represented by a vertex.
For each conflict of the form:
op_i(X) ... op_j(X)
we draw a directed line from node for transaction Ti to transaction Tj.
This means that in all serial schedules equivalent to this schedule, Ti must come before Tj.
If the underlying conflict graph for a schedule has a cycle, then the schedule is not serializable.
If there are no cycles, then we can find a serial order by running topological sort on the conflict graph:
- Find a node with no incoming edges, add to the serial order and remove from the graph until no nodes are left.
Example¶
Given the following schedule:
r1(X) r3(Y) r1(Z) w1(Z) w1(X) r2(Z) r3(X) r2(W) w3(Y) w3(W) Let's find all conflicts first w1(Z) r2(Z) w1(X) r3(X) r2(W) w3(W)
The resulting conflict graph is shown below:

This graph has no cycles and is therefore serializable.
Here is a serial order:
- Node T1 has no incoming edges, so it must come first.
- After we remove T1, node T2 has no incoming edges, so it must come second.
- The final serial order is: T1, T2, T3.
Suppose we are given the following schedule instead:
r1(X) r3(Y) r1(Z) w1(Z) r2(Z) r3(X) w1(X) r2(W) w3(Y) w3(W) Let's find all conflicts again: w1(Z) r2(Z) r3(X) w1(X) r2(W) w3(W)
The resulting conflict graph is shown below:
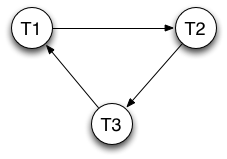
As this graph has cycles, this schedule is not serializable.
Serializable schedules and Concurrency Control¶
We want to make sure that the transaction management system only produces serializable schedules.
This is the main principle behind concurrency control.
Concurrency control is a series of protocols implemented to ensure the resulting schedules are serializable.
We can achieve this in two different ways:
Check before each transaction operation to see if it will lead to a potentially bad schedule.
If the operation can cause trouble, stop the operation and suspend the transaction until it can continue.
Often accomplished using locks (see below).
Let all transactions execute freely, but check before they commit if they may lead to a bad schedule.
If so, abort the transaction and undo any changes it made.
Often accomplished using state information (multi-version concurrency control used in Postgresql using timestamps).
We will see the lock mechanism in detail. We will discuss the multi-version control very briefly afterwards.
Locking based concurrency control schemes¶
Request a lock on a data item before accessing it
If the lock is available, then the transaction can proceed
If the lock is not available, then the transaction is put on hold and will wait until the given lock becomes available
The transaction management system will put the transaction on hold and monitor the lock it needs.
As soon as the locked item is unlocked, the first transaction waiting for that lock is granted the lock and allowed to continue.
We will consider two actions:
l1(X) : transaction T1 locks X u1(X) : transaction T1 unlocks X
Example:
One possible execution with locks.
| T1 | T2 |
|---|---|
| l1(A)r1(A) | |
| w1(X) | |
| l2(A) denied, waiting | |
| l1(B)r1(B) | |
| w1(B)u1(B) | |
| u1(A) | |
| l2(A) granted | |
| r2(A) | |
| w2(A) | |
| u2(A) |
Lock Protocols¶
- Locking alone does not guarantee serializable schedules.
- We need a protocol to tell how long to keep locks.
- Two phase locking and strict two phase locking are two such protocols.
Two phase locking protocol¶
All transactions must get a lock for each item that they need to access.
Each transaction can be in one of two phases:
- Growing phase: If a transaction is in this phase, it can only get new locks.
- Shrinking phase: If a transaction is in this phase, it can only release locks.
As soon as a transaction releases one lock, it enters the shrinking phase. After this point, it cannot get any new locks.
Schedules generatd by two phase locking (2PL) are always serializable.
We can prove this (informally) by considering the conflict graphs.
Proving 2PL produces serializable schedules¶
We will prove that if a schedule is not serializable, we can show that there is no way to generate such a schedule using 2PL.
This is not a formal proof, but a simple sketch to show the logic.
Assume by contradiction that S is a schedule with only two transactions T1 and T2 that
- has a cycle
- was allowed by two phase locking
We will show that such a schedule S cannot exist.
If S has a cycle, there operations in S that conflict with each other to form a cycle. Let's see one such example: r1(X) ... w2(X) .. w1(X) where all three operations conflict with each other This schedule is not possible. 1. r1(X) to occur, T1 must be able to lock X before this 2. w2(X) to occur, T2 must be able to lock X before this and T1 must release it. At this point, T1 is in its shrinking phase and does not have a lock on X. 3. For w1(X) to occur, T1 must get a lock on X again, but it is not allowed in 2PL. Hence, this schedule cannot happen under 2PL.
We can show for all other potential schedules with a cycle, they cannot happen under 2PL because this would require a transaction to get a lock that they did not have after they have entered their shrinking phase, which is not allowed under 2PL.
Deadlocks¶
In all schemes that use locks, it is possible to get deadlocks:
two transactions waiting for locks to be released by each other (or any other cycle of this type)
Methods to deal with deadlocks:
- prevention
- detection
Deadlock prevention¶
- Give each transaction a unique and increasing timestamp when it
starts.
- Wait and die: if an older transaction requests a lock held by a younger transaction then wait, otherwise abort.
- Wound and wait: if an older transaction requests a lock held by a younger transaction then abort the younger transaction.
Deadlock detection¶
- Periodically check which transaction is waiting for which
transaction
- If a cycle exists, abort a transaction in the cycle (choose oldest, youngest depending on desired system properties)
- If a transaction waits too long, then time out and abort the transaction.
Lock types¶
- Use two types of locks to allow more concurrent operations
- S: shared lock or read lock is needed to read an item
- X or W: write lock or exclusive lock is needed to write an item
- Many transactions can read the same item, but only one transaction can write an item and hold an X lock on that item.
Lock compatibility¶
If item A has no locks, whoever asks for an S or X lock can get it.
If item A has an S lock by some transaction, only S locks on this item are granted to other transactions.
the only exception is the transaction holding an S lock may upgrade its lock to write if there are no other S locks on this item (see below 2PL protocol with S/X locks for why)
If item A has an X lock, no other transaction can get a lock on A until this lock is released
| Requested lock | None | S | X |
|---|---|---|---|
| S | Yes | Yes | No |
| X | Yes | No | No |
Two Phase Locking with S/X Locks¶
The two phase locking protocol remains the same.
The transactions must request the appropriate lock and release it eventually.
- Request a read lock before reading and a write lock before writing
As before, a transaction cannot get a lock after it releases any locks
If the transaction is already holding a read lock, request to upgrade to a write lock
This way, the transaction can get a write lock without releasing it first (and avoid going into the shrinking phase)
This is only allowed if no other transaction is holding a read lock on the same item. Otherwise, the transaction has to wait
Example:
sl1(X) r1(X) xl1(Y) w1(Y) u1(X) u1(Y)
Lock upgrade requests can also lead to deadlocks
| T1 | T2 |
|---|---|
| sl1(X)r1(X) | |
| sl2(X)r2(X) | |
| x1(X) denied | |
| xl2(X) denied |
Now T1 and T2 are both waiting for the other one to release the S lock on X, which will not happen as both are suspended.
Update locks¶
- We can introduce a new type of lock to address the problem caused by lock upgrades.
- Update lock works as follows:
- An update lock can be granted to one transaction only. The transaction holding an update lock can later upgrade it to exclusive.
- A transaction must request an update lock before it tries to upgrade its lock from S to X.
- If a transaction holds an update lock, no other transaction may get a new lock on that item.
| Requested lock | S | X | U |
|---|---|---|---|
| S | Yes | No | Yes |
| X | No | No | No |
| U | No | No | No |
Update lock works like a shared lock, but it cannot be shared with another update lock.
Locking scheduler¶
- Transactions do not request locks
- The locking scheduler examines the actions of the transaction and inserts the appropriate lock request before the actions.
- Transactions do not release locks.
- The scheduler releases the locks when the transaction commits or aborts.
Locking table¶
- The locking table lists for each item (that is locked):
- what the lock is
- a bit to indicate that there are transactions waiting for that lock
- a linked list of transactions waiting for that lock.
Releasing locks¶
- When a lock is released, the scheduler decides which transaction
waiting for that lock should get it.
- First-come-first-served: the transaction waiting longest should get it (no starvation)
- Priority to shared locks: grant all shared locks first (can cause starvation)
- Priority to upgrading: first grant updates, then use one of the other protocols.
Committing Transactions¶
- Under 2PL, when a transaction is about to commit, it cannot possibly lead to an unserializable schedule. So, commits are granted.
- If the transaction is holding any locks, they are released.
Strict Two Phase Locking (Strict 2PL)¶
- Strict two phase locking is a more restrictive version of 2PL.
- Strict 2PL:
- A transaction requests locks that it needs before accessing an item.
- If the lock is not available, the transaction will wait until the lock is granted.
- When the transaction commits, all locks it is holding are released.
- Under Strict 2PL, there is no shrinking phase.
- As Strict 2PL is even more restrictive than 2PL, it also guarantees serializability.
- However, it allows for less concurrency as it holds locks longer.
- Lesson: if a lock is not needed, it is better to release it as early as possible. As long as 2PL is satisfied, there is no problem.
Lock granularity¶
Instead of only S/X locks, we can use a multi-level lock hierarchy.
This is especially useful for indices:
- Lock upper level of the index with a higher level lock:
- IX: Intention to change a lower level node
- IS: Intention to read (but not change) a lower level node
- SIX: Intension to read some nodes and change some nodes in the lower level.
- Lock upper level of the index with a higher level lock:
When a new transaction comes, it needs to declare intention on the top.
- If the intention is compatible, it can continue to the lower level.
Example:
Reading the whole index (index scan) requires a full S lock on the index.
Not compatible with X, IX or SIX.
Changing only a single node (inserting a new tuple) requires IX lock in the upper level. Only the leaf node being changed is locked with X.
Another transaction with IX or IS can also access the same upper level node, just not the leaf node.
Multi-version Concurrency Control¶
Often transactions will not access the same information.
There is a high cost for requesting and maintaining locks, resolving deadlocks
Instead we can allow transactions to continue without any upfront checks
Read is never blocked and all reads are for committed values.
Each transaction can read values that were committed at the time they started execution (as if a complete snapshot of the db was generated)
Use timestamps to keep track of which transaction is accessing which data items
Data items can have multiple values (multi-version), though only one is the latest
If a transaction T wants to write data X, but a transaction with a later transaction timestamp has changed it, then T will be aborted.
Because X may have changes that T did not yet see (as it is using an earlier timestamp).
Summary¶
Concurrency control is about making sure that concurrent transactions do not access or modify the same data in a problematic way.
The golden standard is serializability: make sure that a schedule generated by a concurrency control mechanism is guaranteed to produce the same result as a serial schedule: one that executes a single transaction at a time.
Though the ordering of transactions in a serial order is not important, any order is acceptable.
Two check serializability, we only need to ensure that conflicting operations by different transaction can occur in the same order in a serial schedule.
We can do this by constructing the conflict graph and checking if there are cycles.
Two main methods of concurrency control are often used.
Lock based systems (such as in two phase locking) try to prevent bad schedules from happening by checking each action (read/write) for transactions before they occur.
Deadlocks are possible.
Multi-version control systems are less restrictive, allow reads and are restrictive for writes.
May require transactions to be aborted and restarted if there are a lot of conflicting operations.