Lecture 21 - B-tree indices

Lecture 21 - B-tree indices#

Announcements#

  • Homework 5 due tonight

  • Lecture Exercise 21 to be posted at 2pm today, due on wednesday midnight

  • Initial (unofficial) version of the grade db is up

Today’s lecture#

  • Secondary access methods

    • Tree indices

  • B-tree indices

  • Insertion/deletion to B-trees

  • Searching in B-trees

Two variables:

  • Pages ®

  • Tuples®

  • So if X = Tuples®/Pages® then X is the number of tuples per disk page

  • Note that X depends on how large the tuples are

  • Primary access method:read every page of a relation to answer a query

    • Sequential scan

    • Cost: Pages®

  • Secondary access method: an additional access method for a query

    • An index on a number of attributes

  • Each node in a dense index contains an entry for each tuple

    • An entry is the key value (if I index on R(A), then A is the key) and a pointer to the tuple

  • Each node in a sparse index stores an entry for a range of values. Often the upper levels of tree indices are sparse.

load_ext sql

%config SqlMagic.displaylimit = None
%sql --section parks
displaylimit: Value None will be treated as 0 (no limit)
Connecting to 'parks'
%%sql 

SELECT 
   pt.tablename
    , pc.reltuples
    , pc.relpages
FROM   
    pg_class pc
    , pg_tables pt
WHERE  
    pt.tableowner=user
    and pt.tablename not like 'pg%'
    and pt.tablename = pc.relname
order by pc.relpages desc;
Running query in 'parks'
22 rows affected.
tablename reltuples relpages
places 531.0 112
place_tags 3261.0 35
people 222.0 32
people_facts 1130.0 21
place_relatedparks 565.0 19
people_tags 1593.0 17
people_relatedparks 249.0 12
park_topics 541.0 9
sql_features 755.0 8
people_images 149.0 7
park_images 151.0 7
parks 32.0 6
park_activities 394.0 5
park_hours 137.0 2
park_emails 32.0 1
park_phoneno 41.0 1
park_addresses 64.0 1
sql_implementation_info 12.0 1
sql_sizing 23.0 1
sql_parts 11.0 1
park_states 75.0 1
output_lines 0.0 0 
%%sql


select 
    relpages
    , relname 
from 
    pg_class 
where 
    relname not like 'pg%' 
    and relpages>0;
Running query in 'parks'
36 rows affected.
relpages relname
2 parks_pkey
13 park_topics_pkey
6 parks
9 park_topics
1 park_addresses
7 park_images
5 pimpk
2 park_phoneno_pkey
1 park_phoneno
2 park_emails_pkey
1 park_emails
2 park_states_pkey
1 park_states
5 park_activities
4 park_hours_pkey
2 park_hours
19 place_relatedparks
35 place_tags
7 places_pkey
112 places
44 place_tags_pkey
10 plrpk
5 people_pkey
22 people_tags_pkey
32 people
17 people_tags
12 people_relatedparks
6 perpk
22 people_facts_pkey
21 people_facts
7 people_images
6 pipk
1 sql_parts
8 sql_features
1 sql_implementation_info
1 sql_sizing

Suppose I create an index on places(placeid)

where placeid is 36 bytes a tuple pointer is 10 bytes

For each tuple, I need 46 bytes

TUPLES(places) = 531

A disk page is 8000 bytes (assume)

8000/(46) approx= 170 tuples per page

531/170 approx= 4 pages of index

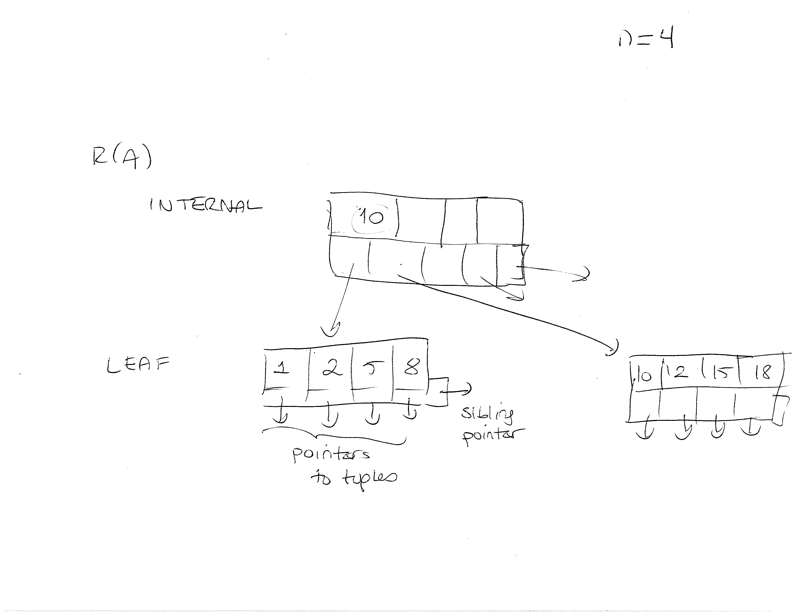
B-tree indices#

  • Secondary access method on a key value, R(A) or R(A,B)

  • Each node in the B-tree is a disk page, stored on disk

  • Leaf nodes of the B-tree are dense, leaf nodes store on entry per tuple

    • An entry: a key value + a disk page pointer (points to a tuple)

  • Internal nodes of the B-tree are sparse, they point to the B-tree nodes in the level below.

    • Each entry is a key value and a disk page pointer (points to a B-tree node page)

  • Leaf nodes have an extra pointer to the next node in the leaf to the right (sibling pointers)

  • Each node in the B-tree has a maximum capacity, which we call n: maximum number of key value and pointer pairs I can store in a page

  • Each node (except root) has a minimum capacity, floor((n+1)/2) entries

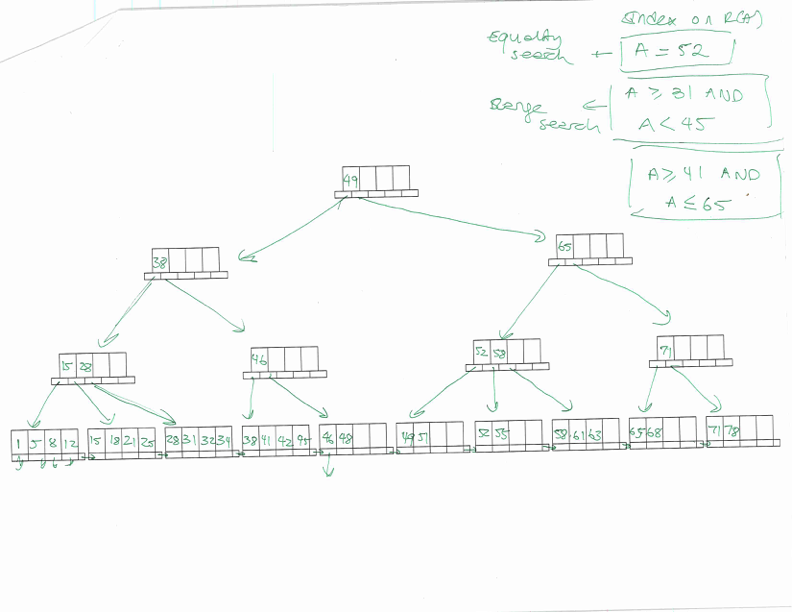
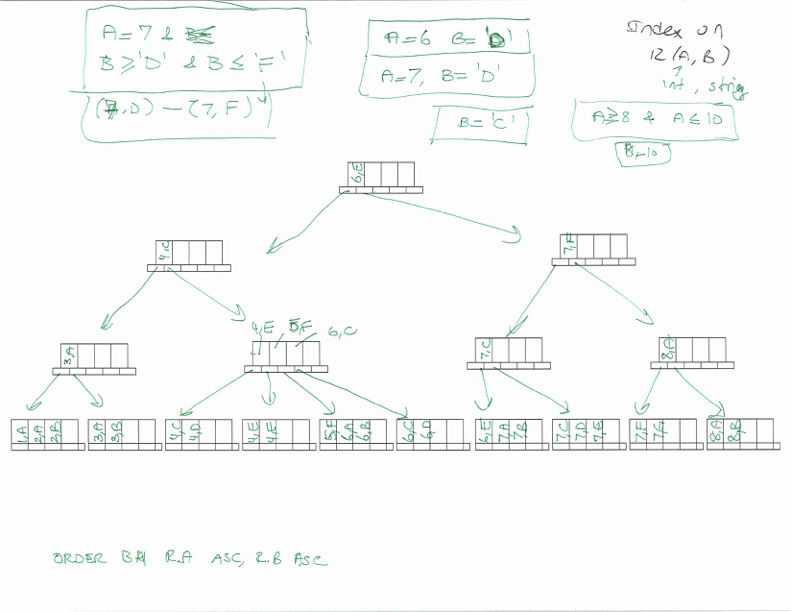
Searching in B-trees#

Searching key = value

  • Start from root, find the internal node in the next level until you reach the leaf level

  • If the value is found, return the key value and tuple address

Searching key in range [A,B]

  • Start from root searching for the first leaf node >=A, find the internal node in the next level until you reaach the leaf level.

  • Scan the leaf level using sibling pointers until you find the first leaf node greater than B.

  • Output all found key values and associated tuple pointers

x x x

Contents