CGAL::Iso_cuboid_3<R>

Definition

³

Although they are represented in a canonical form by only two vertices, namely the lexicographically smallest and largest vertex with respect to Cartesian $$xyz coordinates, we provide functions for ``accessing'' the other vertices as well.

Iso-oriented cuboids and bounding boxes are quite similar. The difference however is that bounding boxes have always double coordinates, whereas the coordinate type of an iso-oriented cuboid is chosen by the user.

Creation

Iso_cuboid_3<R> c ( Point_3<R> p, Point_3<R> q);
	introduces an iso-oriented cuboid c with diagonal opposite vertices $$p and $$q. Note that the object is brought in the canonical form.
Iso_cuboid_3<R> c ( RT min_hx, RT min_hy, RT min_hz, RT max_hx, RT max_hy, RT max_hz, RT hw = R::RT(1));
	introduces an iso-oriented cuboid c with diagonal opposite vertices (min_hx/hw, min_hy/hw, min_hz/hw) and (max_hx/hw, max_hy/hw, max_hz/hw). If the last argument is not explicitly given, it defaults to R::RT(1). Precondition: hw $$ R::RT(0)

Operations

bool	c.operator== ( c2)
		Test for equality: two iso-oriented cuboid are equal, iff their lower left and their upper right vertices are equal.
bool	c.operator!= ( c2)
		Test for inequality.
Point_3<R>	c.vertex ( int i)	returns the i'th vertex modulo 8 of c. starting with the lower left vertex.
Point_3<R>	c.operator[] ( int i)
		returns vertex(i), as indicated in the figure below:

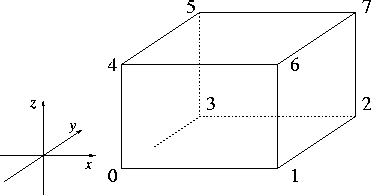
Point_3<R>	c.min ()	returns the smallest vertex of c (= vertex(0)).
Point_3<R>	c.max ()	returns the largest vertex of c (= vertex(7)).
FT	c.xmin ()	returns smallest Cartesian $$x-coordinate in c.
FT	c.ymin ()	returns smallest Cartesian $$y-coordinate in c.
FT	c.zmin ()	returns smallest Cartesian $$z-coordinate in c.
FT	c.xmax ()	returns largest Cartesian $$x-coordinate in c.
FT	c.ymax ()	returns largest Cartesian $$y-coordinate in c.
FT	c.zmax ()	returns largest Cartesian $$z-coordinate in c.
FT	c.min_coord ( int i)
		returns $$i-th Cartesian coordinate of the smallest vertex of c. Precondition: $$0 i 2.
FT	c.max_coord ( int i)
		returns $$i-th Cartesian coordinate of the largest vertex of c. Precondition: $$0 i 2.

Predicates

bool	c.is_degenerate ()	c is degenerate, if all vertices are collinear.
Bounded_side	c.bounded_side ( Point_3<R> p)
		returns either ON_UNBOUNDED_SIDE, ON_BOUNDED_SIDE, or the constant ON_BOUNDARY, depending on where point $$p is.
bool	c.has_on_boundary ( Point_3<R> p)
bool	c.has_on_bounded_side ( Point_3<R> p)
bool	c.has_on_unbounded_side ( Point_3<R> p)

Miscellaneous

FT	c.volume ()	returns the volume of c.
Bbox	c.bbox ()	returns a bounding box containing c.
Iso_cuboid_3<R>	c.transform ( Aff_transformation_3<R> t)
		returns the iso-oriented cuboid obtained by applying $$t on the smallest and the largest of c. Precondition: The angle at a rotation must be a multiple of $$/2, otherwise the resulting cuboid does not have the same size. Note that rotating about an arbitrary angle can even result in a degenerate iso-oriented cuboid.

See Also