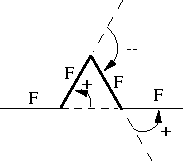
Figure 1: The Koch curve. The angle increment is 60 degrees.
CS 66.460
Introduction to Graphical Human-Machine Interfaces
Spring 1997
Programming Project #2
Java Programmimg
DUE: WEDNESDAY, APRIL 30, 1997 BY 11:59PM
For this project you will implement an applet that will render an L-system. Much of the code will be given to you in the form of other example applets. So, you will only need to come up with a minor amount of new Java code. In addition, the two example applets provided will contain code that you can use or extend when creating your own applet.
What are L-systems, you ask? An L-system or Lindemayer system is a formal grammar for generating strings. (That is, it is a collection of rules such as replace X with XYX.) By recursively applying the rules of the L-system to an initial string, a string with fractal structure can be created. Interpreting this string as a set of graphical commands allows the fractal to be displayed. L-systems are very useful for generating realistic plant structures.
Formally, we describe an L-system by a tuple:
To generate an L-system string, you start with the axiom and replace symbols in the axiom with the right hand side of a production if one exists. This can be done for a specified number of iterations, generating longer and longer strings.
For example, consider the following L-system:
ANGLE = 60 degrees AXIOM = F RULES : F -> F+F--F+FSo starting with the axiom we can generate different ``orders'' of the L-system:
Order 0: F
1: F+F--F+F
2: F+F--F+F+F+F--F+F--F+F--F+F+F+F--F+F
3: ...
At each iteration, we only have one rule, to replace F by
F-F++F-F. The symbols in the alphabet have special meaings. For our
applet, we will use the following turtle alphabet:
f make the turtle move (jump) forward without drawing F make the turtle draw forward + turn left by angle - turn right by angle | turn around (rotate by 180 degrees) ! reverse directions (switch meanings of +, -, /, \) \(x) roll the turtle left (increase current angle) by x (degrees) /(x) roll the turtle right (decrease current angle) by x (degrees) cRRGGBB set turtle pen color to RGB color RRGGBB <(x) darken turtle pen color by x (percentage) >(x) darken turtle pen color by x (percentage) w(x) set the width of the line drawn by the turtle to x (integer) [ push a turtle onto the turtle stack ] pop a turtle onto the turtle stackThis is the Koch curve, shown in the first order in Figure 1. At higher orders, each of the F line segments are replaced with the same curve, leading to a recursively generated picture!

Figure 1: The Koch curve. The angle increment is 60 degrees.
So once a string has been generated, it can be passed to a render routine to make the turtle draw it. The render routine simply scans the generated string from left to right and based on the symbol scanned, instructs the turtle to do something based on the symbol's meaning from the turtle alphabet.
Turtles begin with a pre-set, but user customizable:
Your goal for this project is to implement an L-system applet in Java. There are two parts to this project:
Your interface, which you will implement with the Java AWT library, will consisit of a number of buttons, labels, and text fields and also drawing surfaces. You will probably want to use panels to help you layout the various interface elements.
Your use interface should allow the user to do the following:
You may also wish to allow the user to input:
Take a look at the code in the example LsystemGen applet which shows how to add the rules, axiom, and other information to an instance of the Lsystem class.
The skeleton for this routine has been provided for you. The routine is part of the TurtleCanvas class which has been given to you as part of the TurtleDraw applet. Within this class is the routine:
TurtleCanvas.renderLsystem (Graphics g, String path);You need to code the big switch statement, as we discussed in class, to make the turtle respond to the symbols seen in the string (the string is the parameter path].
So how do these two parts work together? The user of your applet will specify the axiom, the order, and then add at least one rule by specifying the predecessor and successor for each rule and adding it to the L-system.
Once the rules have been entered the user can press the generate button, which creates an L-system and generates the path string for the number of iterations indicated by the order. The other information like the start and rotate angles, turtle length, etc are also taken into account when generating the string. The string is then passed to the renderLsystem(String path) routine so that it may be displayed.
You have been given two Java applets.
This applet allows you to command a turtle to move around a drawing canvas. You can make the turtle move, draw, rotate, change color, etc. You can also change turtle parameters such as (length, width, and rotation angle) as well as the start angle and the x- and y- scales.
In this applet you can find all the code needed to make the turtle draw on a canvas.
This applet allows the user to specify an L-system and then generate the strings based on the number of iterations specified. It will display the resulting string in a TextArea but it does not draw the string with turtles.
In this applet you can find all the code needed to create and manipulate L-systems.
These applets (and their source!) can be found on the Web at:
http://www.cs.rpi.edu/courses/spring97/GHMI/project2/
Be sure you grab all of the .java and .html files for each applet and place them in their own directories.
Before you start to write your applet, you should compile these with the java compiler and either run them with the appletviewer or from your Web browser. It would be a good idea to print out all of the java source files and study them. Play with the example programs and try to understand which parts of the code do what. Then, start designing and implementing your applet.
You should find almost all of the code you need in these example programs. You may want to splice code from the two examples to create your applet. You may also want to create a little bit different interface, but the examples should show you how to use the AWT components you need.
You are to submit the following:
This file will contain the APPLET tag which will run your compiled applet.
This file will describe how to use your applet and contain a link to the HTML file (above) that runs your applet.
You should experiment with your applet and try to come up with some interesting L-systems. Make up rules, explore! In your HTML report, list any L-systems you found, by listing its axiom and its rules and any other parameters you used. If you feel adventurous you might figure out how to create a GIF/JPG of the generated output and put it a link to it in your report also.
Make sure you specify the URL to where your HTML file is located from your own home page.
There will be NO DEMOs for this project, since we will be able to compile and run your applets with your checked-in code.
The Lsystem class is capable of using stochastic rules. This means that you can have more than one rule for the same symbol. However, each rule is given a probability, so that one of the rules can be chosen randomly based on the probabilities. Here is one stochastic L-system:
AXIOM : S=F
RULES : F=(.10)cff0000F[+F]F[-F]F
F=(.45)c00ff00F[+F]F
F=(.45)c0000ffF[-F]F
START ANGLE : 270 (degrees)
ROTATE ANGLE : 45 (degrees)
ORDER : 5
And here is another one you might try (not stochastic):
AXIOM : F
RULES : F=F[+F]F[-F][F]
START ANGLE : 270 (degrees)
ROTATE ANGLE : 22.5 (degrees)
ORDER : 5