Lecture 11 — Decisions Part 2¶
Overview — Logic and Decision Making, part 2¶
- In this lecture, we will first talk about program structure and debugging.
- Then, we will talk about logic in more detail.
- Logic is the key to getting programs right
- Boolean logic
- Nested if statements
- Assigning booelan variables
Part 1: Program Structure¶
Programming requires four basic skills:
- Develop a solution.
- Start with small steps, solve them and then add complexity
- Structure your code.
- Abstract out repeated code into functions.
- Make your code easy to read and modify. Use meaningful variable names and break complex operations into smaller parts.
- Do not hard code values so that it is easy to change the program.
- Include comments for important functions, but do not clutter your code with unnecessary comments. If a function makes an assumption on validity or type of inputs, this is a good thing to document in your code.
- If your function is meant to return a value, make sure it always returns a value.
- Test your code.
- Find all possible cases that your program should work for. As programs get larger, this is increasing hard.
- If you cannot check for all inputs, then you must then check your code for meaningful inputs: regular (expected inputs) and edge cases (inputs that can break your code).
- Debug your code.
- Never assume an untested part of your code is bug free.
- Learn syntax well so that you can spot and fix syntax errors fast.
- Semantic errors are much harder to find and fix. You need strategies to isolate where the error is.
- Print output before and after crucial steps.
- Look at where your program crashed.
- Use a debugger.
- Simplify the problem. Remove parts of your code until you no longer have error.
- Test parts of your code separately and once you are convinced they are bug free, concentrate on other parts.
We will attempt to write an unbreakable program in today’s lecture.
Help with debugging: Infinite Loops and Other Errors¶
One important danger with
whileloops is that they may not stop!For example, it is possible that the following code runs “forever”. How?
n = int(raw_input("Enter a positive integer ==> ")) sum = 0 i = 0 while i != n: sum += i i += 1 print 'Sum is', sum
How might we find such an error?
- Careful reading of the code
- Insert print statements
- Use the Wing IDE debugger.
We will practice with the Wing IDE debugger in class, using it to understand the behavior of the program. We will explain the following picture
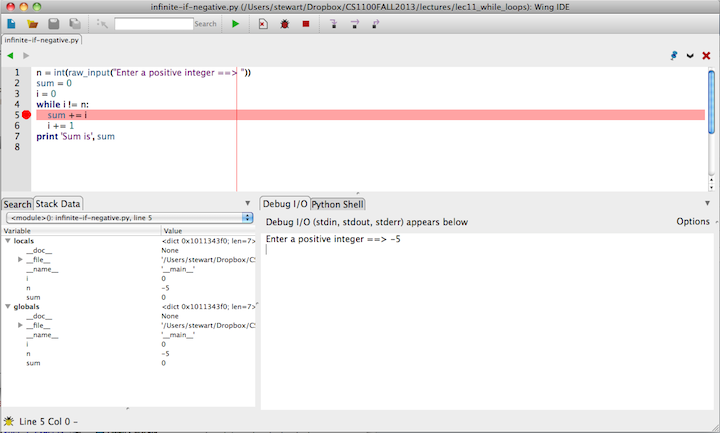
and note the use of
- The hand, bug and stop symbols on the top of the display, and
- The Debug I/O and Stack Data at the bottom of the display.
Debugging becomes crucial in tracking logic errors as well as we will see.
Program organization¶
Visualize code as having two main parts: the main body and the functions that help the main code.
Make sure your functions do only one thing, so they are easy to test and can be in many places.
We will discuss the above by going through the following example. Note the new addition to the program structure:
if __name__ == "__main__" # Put the main body of the program below this lineWhen we execute a program, the above line has no effect. But it helps to separate main body of the program from the function definitions.
When we import a program in another code (like the utility code I have been giving you), any code below the above line is skipped!
This allows programs to work both as modules and stand alone code. It is best to use this section for test code for your modules.
Example: Random Walk¶
Many numerical simulations, including many video games involve random events.
Python includes a module to generate numbers at random. In particular,
import random # Print three numbers randomly generated between 0 and 1. print random.random() print random.random() print random.random() # Print a random integer in the range 0..5 print random.randint(0,5) print random.randint(0,5) print random.randint(0,5)
We’d like to use this to simulate a “random walk”:
- Hypothetically, a (very drunk) person takes a step to the left or a step to the right, completely at random (equally likely to go left or right), in one time unit.
- If the person is on a platform with
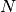 steps and the person
starts in the middle, this process is repeated until s/he falls
off (reaches step 0 or step
steps and the person
starts in the middle, this process is repeated until s/he falls
off (reaches step 0 or step 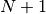 )
) - How long does this take?
Many variations on this problem appear in physical simulations.
We can simulate a steps in two ways:
- If
random.random()returns a value less than 0.5 step to the left; otherwise step to the right. - If
random.randint(0,1)returns 0 then step left; otherwise, step right.
- If
We’ll write the code in class, starting from the following:
import random # Print the output def print_platform( iteration, location, width ): before = location-1 after = width-location platform = '_'*before + 'X' + '_'*after print "%4d: %s" %(iteration,platform), raw_input( ' <enter>') # wait for an <enter> before the next step ####################################################################### if __name__ == "__main__" # Get the width of the platform n = int( raw_input("Input width of the platform ==> ") )
Review: Boolean Logic¶
- Invented / discovered by George Boole in the 1840’s to reduce
classical logic to an algebra
- This was a crucial mathematical step on the road to computation and computers.
- Values (in Python) are
TrueandFalse - Operators
- Comparisons:
<, >, <=, >=, == != - Logic:
and,or,not
- Comparisons:
Truth Tables¶
Aside to recall the syntax:
and,or,notare lower case!If we have two boolean expressions, which we will refer to as
ex1andex2, and if we combine their “truth” values usingandwe have the following “truth table” to describe the resultex1ex2ex1 and ex2FalseFalseFalseFalseTrueFalseTrueFalseFalseTrueTrueTrueIf we combine the two expressions using
or, we haveex1ex2ex1 or ex2FalseFalseFalseFalseTrueTrueTrueFalseTrueTrueTrueTrueFinally, using
notwe haveex1not ex1FalseTrueTrueFalse
DeMorgan’s Laws Relating and, or, not¶
Using
ex1andex2once again to represent boolean expressions, we havenot (ex1 and ex2) == (not ex1) or (not ex2)
And,
not (ex1 or ex2) == (not ex1) and (not ex2)
Also, distribution laws
ex1 and (ex2 or ex3) == (ex1 and ex2) or (ex1 and ex3) ex1 or (ex2 and ex3) == (ex1 or ex2) and (ex1 or ex3)
We can prove these using truth tables.
Why Do We Care?¶
- When we’ve written logical expressions into our programs, it no longer matters what we intended; it matters what the logic actually does.
- For complicated boolean expressions, we may need to almost prove that they are correct
- We will work through the example of writing a boolean expression to decide whether or not two rectangles with sides parallel to each other and to the x and y axes intersect.
Short-Circuited Boolean Expressions¶
Python only evaluates expressions as far as needed to make a decision.
Therefore, in boolean expression of the form
ex1 and ex2
ex2will not be evaluated ifex1evaluates toFalse. Think about why.Also, in boolean expression of the form
ex1 or ex2
ex2will not be evaluated ifex1evalues toTrue.This “short-circuiting” is common across many programming languages.
Let’s try to check for valid input.
x = raw_input("Enter a positive number ==> ")
Part 1 Exercises¶
Write a boolean expression to determine if two circles, with centers at locations
x0,y0andx1,y1and radiir0andr1intersect.Suppose you have a tuple that stores the semester and year a course was taken, as in
when = ('Spring',2013)
Write a function that takes two such lists as arguments and returns
Trueif the first list represents an earlier semester andFalseotherwise. The possible semesters are'Spring'and'Fall'.
Part 2 — More Complicated/Nest If Statements¶
We can place
ifstatements inside of otherifstatements.To illustrate
if ex1: if ex2: blockA elif ex3: blockB elif ex4: blockD else: blockE
We can also work back and forth between this structure and a single level
if,elif,elif,elsestructure.We will work through this example in class.
Example: Ordering Three Values¶
- Suppose three siblings,
Dale,ErinandSam, have heights stored in the variableshd,heandhs, respectively . - We’d like code to print the names in order of height from greatest to least.
- We’ll consider doing this with nested
ifstatements and with a single-levelif,elifstructure.
Part 2 Exercise¶
In the following code, for what values of
xandydoes the code print 1, for what values does the code print 2, and for what values does the code print nothing at all?if x>5 and y<10: if x<5 or y>2: if y>3 or z<3: print 1 else: print 2
The moral of the story is that you should be careful to ensure that your logic and if structures cover the entire range of possibilities!
Check that a string contains a float.
Suppose we represent the date as three integers in a tuple giving the month, the day and the year, as in
d = (2, 26, 2103)
Write a Python function called
is_earlierthat takes two date lists and returnsTrueif the first date,d1is earlier than the second,d2. It should returnFalseotherwise. Try to write this in three different ways:- Nested ifs,
- if - elif - elif - else,
- A single boolean expression.
Part 3: Storing Conditionals¶
Sometimes we store the result of boolean expressions in a variable for later use:
f = float(raw_input("Enter a Fahrenheit temperature: ")) is_below_freezing = f < 32.0 if is_below_freezing: print "Brrr. It is cold"
We use this to
- Make code clearer
- Avoid repeating tests
Example from the Textbook¶
Doctors often suggest a patient’s risk of heart disease in terms of a combination of the BMI (body mask index) and age using the following table:
Age 
Age 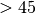
BMI 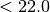
Low Medium BMI 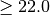
Medium High Assuming the values for a patient are stored in variables
ageandbmi, we can write the following codeslim = bmi < 22.0 young = age <= 45 if young: if slim: risk = 'low' else risk = 'medium' else: if slim: risk = 'medium' else: risk = 'high'
Part 3 Exercises¶
- Rewrite the previous code without the nested if’s. There are several good solutions.
- Make the code for checking whether two circles intersect unbreakable.
- Write code to check if two rectangles intersect.
Summary¶
- Logic is a crucial component of every program.
- Basic rules of logic, including DeMorgan’s laws, help us to write and understand boolean expressions.
- It sometimes requires careful, precise thinking, even at the level of
a proof, to ensure logical expressions and if statement structures
are correct.
- Many bugs in supposedly-working programs are caused by conditions that the programmers did not consider.
- If statements can be structured in many ways, often nested several
levels deep.
- Nesting deeply can lead to confusing code, however.
- Warning specifically for Python: you can easily change the meaning of your program by accidentally changing indentation. It is very hard to debug these changes.
- Using variables to store boolean values can make code easier to understand and avoids repeated tests.
- Make sure your logic and resulting expressions cover the universe of possibilities!