Lecture 23 — Recursion¶
Overview¶
- When a function calls itself, it is known as a recursive function.
- Use of the function call stack allows Python to handle recursive functions correctly.
- Examples include factorial, Fibonacci, greatest common divisor, binary search and mergesort.
- We’ll think about how to hand-simulate a recursive function as well as rules for writing recursive functions.
Our First Example¶
Consider the following Python function.
def blast(n): if n > 0: print n blast(n-1) else: print "Blast off!"
What is the the output from the call?
blast(5)
Python’s Call Stack Mechanism¶
The following mechanism helps us understand what is happening:
- Each time your code makes a function call, Python puts information on
the “call stack”, including
- All values of parameters and local variables
- The location in the code where the function call is being made.
- Python then makes the function call, switching execution to the start of the called function.
- This function in turn can make additional, potentially recursive, function calls, adding information to the top of the stack each time.
- When a function ends, Python looks at the top of the stack, and
- restores the values of the local variables and parameters of the most recent calling function,
- removes this information from the top of the stack,
- inserts the returned value of the called function (if any) in the appropriate location of the calling function’s code, and
- continues execution from the location where the call was made.
Exercise¶
What is the output of the following?
def rp1( L, i ):
if i < len(L):
print L[i],
rp1( L, i+1 )
else:
print
def rp2( L, i ):
if i < len(L):
rp2( L, i+1 )
print L[i],
else:
print
L = [ 2, 3, 5, 7, 11 ]
rp1(L,0)
rp2(L,0)
Note that the entirety of list L is not copied to the top of the
stack. Instead, a reference (an alias) to L is placed on the stack.
Factorial¶
The factorial function is
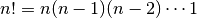
and
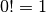
This is an imprecise definition because the :math:` cdots ` is not formally defined.
Writing this recursively helps to clear it up:
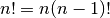
and
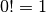
The factorial is now defined in terms of itself, but on a smaller number!
Note how this definition now has a recursive part and a non-recursive part:
- The non-recursive part is called the base case. There can be more than one of these, but there must be at least one!
Exercise¶
- Write a recursive Python function to implement
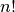 .
. - Hand-simulate the call stack for
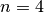 .
.
We’ll add output code to the implementation to help visualize the recursive calls in a different way.
Rules for Writing Recursive Functions¶
- Define the problem you are trying to solve in terms of smaller /
simpler instances of the problem. This includes
- What needs to happen before making a recursive call?
- What recursive call(s) must be made?
- What needs to happen to combine or generate results after the recursive call (or calls) ends?
- Define the base case or cases.
- Make sure the code is proceeding toward the base case in every step.
Fibonacci¶
The Fibonacci sequence starts with the values 0 and 1.
Each new value in the sequence is obtained by adding the two previous values, producing
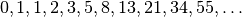
Recursively, the
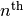 value,
value, 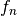 , of the
sequence is defined as
, of the
sequence is defined as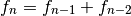
This leads naturally to a recursive function, which we will complete in lecture.
Dangers of Recursion¶
- Some recursive function implementations contain wasteful repeated computation.
- Recursive function calls — like any function calls — typically involve hidden overhead costs.
- Often, therefore, a recursive functions can (and should) be replaced with a non-recursive, iterative function that is significantly more efficient.
Exercise¶
- Write a non-recursive function to compute
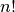 .
. - Write a non-recursive function to compute the
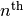 Fibonacci number. Be sure to avoid the wasted computation of the
recursive version.
Fibonacci number. Be sure to avoid the wasted computation of the
recursive version.
Why, Then, Do We Study Recursion?¶
- Many of our definitions and even, our logical structures (such as lists), are formalized using recursion.
- Sometimes recursive functions are the first ones we come up with and
the easiest to write (at least after you are comfortable with
recursion).
- Only later do we write non-recursive versions.
- Sometimes on harder problems it is harder to write non-recursive functions directly.
Example 1¶
Fractals are often defined using recursion. How do we draw a Sierpinski triangle like the one shown below?
Define the basic principle
Define the recursive step
def draw_sierpinski( ):
Example 2¶
Remember the lego homework? We wanted to find a solution based on mix and match. While a non-recursive solution exists, the recursive solution is easier to formulate.
Given a list of legos and a lego we would like match:
Define the basis step(s): when should we stop?
Define the recursive step
def match_lego(legolist, lego):
Last Two Examples¶
- Binary Search
- Merge Sort
Binary Search¶
Consider the following recursive version of binary search:
def binary_search_rec( L, value, low, high ): if low == high: return L[low] == value mid = (low + high) / 2 if value < L[mid]: return binary_search_rec( L, value, low, mid-1 ) else: return binary_search_rec( L, value, mid, high ) def binary_search(L, value): return binary_search_rec(L, value, 0, len(L)-1)
Here is an example of how this is called:
print binary_search( [ 5, 13, 15, 24, 30, 38, 40, 45], 13 )
Note that we have two functions, with
binary_searchacting as a “driver function” ofbinary_search_recwhich does the real work.- This notion of a driver function is common to recursion because it is used to set up the bounds of the recursion, which the original calling code does not and should not have to know about.
Is the code right?
- No! What rule of recursion did we violate?
- Fortunately, the fix is easy, as we will see.
Merge Sort¶
The fundamental idea of merge sort is recursive:
- Split the list in half
- Recursively sort each half
- Merge the result
We repeat our use of the
mergefunction from Lecture 20:def merge(L1,L2): i1 = 0 i2 = 0 L = [] while i1<len(L1) and i2<len(L2): if L1[i1] < L2[i2]: L.append(L1[i1]) i1 += 1 else: L.append(L2[i2]) i2 += 1 L.extend(L1[i1:]) L.extend(L2[i2:]) return L
Using this, we will write the main
merge_sortfunction in class.def merge_sort(L):
- The solution will be posted on-line.
Comparing what we write to our earlier non-recursive version of merge sort shows that the primary job of the recursion is to organize the merging process!
Summary¶
- Functions that call themselves are known as “recursive functions”
- Use of a function call stack allows Python to handle recursive functions correctly.
- Many structures and functions important to computer science are defined recursively.
- Fundamentally, recurision is about defining a problem solution as a function of the solution to a simpler/shorter/smaller version of the problem.
- A basis case (or cases) is (are) always needed to make a recursion function succeed.
- Infinite recursion is avoided by ensure that progress is made toward the basis case or cases in every recursive call.
- While many recursive functions are easily rewritten to remove the recursion, some advanced problems are difficult to solve without recursion.
Additional Practice Exercises¶
Attempts to define the formal foundations of mathematics at the start of the 20th century depended heavily on recursion. While ultimately completing this formalization was shown to be impossible, the work led to much of the formal basis of computer science. Here is an example of the definition of adding two non-negative integers based on just +1 and -1 operations (formally known as successor and predecessor operations) and equality tests:
def add(m,n): if n == 0: return m else: return add(m,n-1) + 1
Show the sequence of calls made by
print add(5,3)
and then show the return values resulting from each recursive call.
Following the ideas from the previous problem, write a recursive function to multiply two non-negative integers using only the
addfunction we’ve just defined, together with +1, -1 and equality tests.Now, define the integer power function,
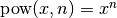 , in terms of the
, in terms of the multfunction you just wrote, together with +1, -1, and equality.Euclid’s algorithm for finding the greatest common divisor is one of the oldest known algorithms. If
 and
and 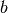 are positive
integers, with
are positive
integers, with 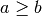 , then let
, then let  be the remainder
of dividing
be the remainder
of dividing  by
by 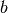 . If
. If 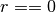 , then
, then 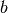 is the GCD of the two integers. Otherwise, the GCD of
is the GCD of the two integers. Otherwise, the GCD of  and
and
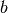 equals the GCD of
equals the GCD of 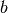 and
and  . Here is the
Python code:
. Here is the
Python code:def gcd(a,b): if a < b: a,b = b,a r = a % b if r==0: return b else: return gcd(b,r)
What is the output of
print gcd(36,24) print gcd(84,65) print gcd(84,66)
Why do we know that
gcdis proceeding toward the base case (as required by our “rules” of writing recursive functions)?
Specify the recursive calls and return values from our
merge_sortimplementation for the listL = [ 15, 81, 32, 16, 8, 91, 12 ]
