|
CSCI 4530/6530 Advanced Computer Graphics Spring 2017 |
Home
Contact Information
Office Hours
Announcements
LMS (Discussion Forum)
Syllabus
Prerequisites
References
Grading
Assigned Readings
Paper Discussant
Calendar
Lecture notes
Readings
Homework
Practice Quizzes
Homework
Collaboration Policy
Homework Late Policy
Compilers
Graphics library notes
CMake notes
memory debugging
Submitty
Final Project
Spring '15 Projects
Spring '14 Projects
Spring '13 Projects
Spring '12 Projects
Spring '11 Projects
Spring '10 Projects
Spring '09 Projects
Spring '08 Projects
Spring '07 Projects
Assignment 2: Cloth & Fluid Simulation
The goal of this assignment is to implement and experiment with two different physical simulation engines: a spring-mass cloth system and a grid-based fluid system. The bulk of the rendering, visualization, and interaction code including the basic data structures is provided.
In the cloth simulation a 2D grid of point masses are connected with structural, shear, and flexion/bend springs. To mitigate the "super-elastic" effect of these springs without increasing the stiffness (which requires a smaller timestep) you will implement the correction term described in "Deformation Constraints in a Mass-Spring Model to Describe Rigid Cloth Behavior", Xavier Provot, 1995.
For the fluid simulation, you will track a collection of marker particles as they move through a 3D grid of cells, monitoring the cell pressure and velocity through each face of each cell. The implementation requires tri-linear interpolation of the velocities, handling free-slip and no-slip boundary conditions, and adjustment for incompressible flows as described in "Realistic Animation of Liquids", Foster and Metaxas, Graphics Interface 1996.
Tasks
-
Download the provided source code and the sample test datasets. Compile it on your favorite platform and try the command lines below. There are a number of visualization options for the cloth system. Press 'm' to toggle drawing of the masses/particles in the spring-mass particle system. Press 'w' to toggle drawing of the wireframe (springs). Press 's' to toggle drawing of the surface represented by the masses & springs. 'v' and 'f' are used to toggle visualizations of the velocity and forces at each mass position. Finally, 'b' is used to toggle the bounding box of the original mass positions.
-
First implement basic animation of the masses. You'll need to compute the spring forces and track the position, velocity, and acceleration of each particle as time progresses. Simple forward/explicit Euler integration is sufficient. You can access the timestep and gravity from the ArgParser class. Initially test your code on the small example shown below and verify that each of the spring forces (structural, shear, and bend/flexion) and the force due to gravity are correct. Pressing 'a' will toggle the animation on and off. Each loop of this continuous animation will call Cloth::Animate() 10 times and then refresh the screen. To take just one step of animation, press the space bar. You can restart the animation from the beginning by pressing 'r'.
./simulation -cloth ../src/small_cloth.txt -timestep 0.001
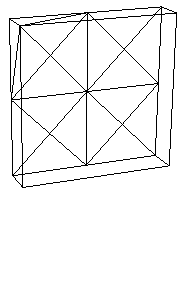
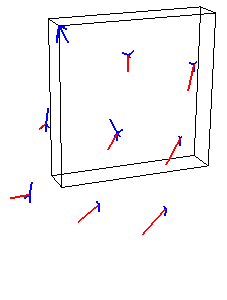

You will need to complete the implementation for the force visualization. Your visualization does not need to match the one above (the blue lines), as long as you find its output informative and helpful in your debugging.
-
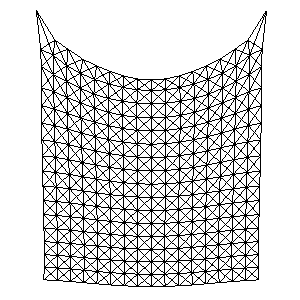
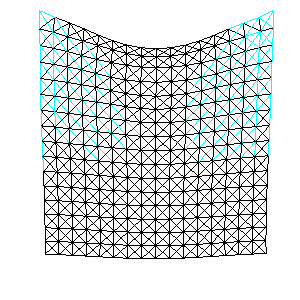
Once your basic spring-mass system is working, test it on the larger example below. As illustrated by Provot, the springs at the corner will stretch too much. Implement the iterative correction/adjustment method for springs that have stretched beyond the specified threshold. The provided code will visualize the "over-stretched" springs in cyan (shown below).
./simulation -cloth ../src/provot_original.txt -timestep 0.001 ./simulation -cloth ../src/provot_correct_structural.txt -timestep 0.001 ./simulation -cloth ../src/provot_correct_structural_and_shear.txt -timestep 0.001




-
When you are confident that your implementation is complete, test it on the examples below which use different parameter values to mimic different types of cloth. Now experiment with your system and try adjusting the many different parameters. How stable is the simulation? Discuss in your README.txt. Make at least one interesting new test scene. You may extend the input file format as necessary for your new example(s). Describe your new example and how to run it in your README file.
./simulation -cloth ../src/denim_curtain.txt -timestep 0.001 ./simulation -cloth ../src/silk_curtain.txt -timestep 0.001
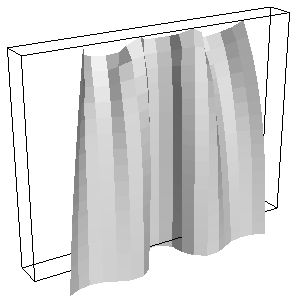
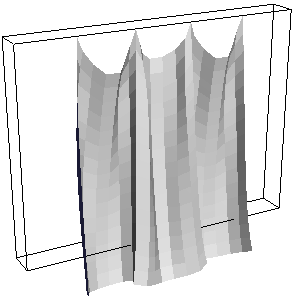
./simulation -cloth ../src/table_cloth.txt -timestep 0.005

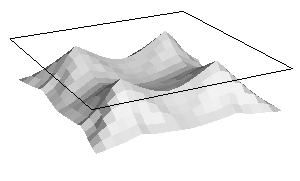

-
In your experimentation, you undoubtedly caused the cloth to "explode" at least once. In theory this instability can always be fixed by using a smaller timestep. So now, let's implement an adaptive timestep for the simulator. Start with the timestep provided on the command line, but if the simulation is too stiff (unstable at that timestep), back up, halve the timestep, and try again. What criteria did you use to detect that the system is unstable? Discuss in your README.txt
-
Now for the second part --- fluid simulation, which is launched like this:
./simulation -fluid ../src/fluid_random_xy.txt -timestep 0.01
The images below show some visualizations of this dataset of random particles on a 5x5x1 grid. On the left we see the random particles (approximately 64 per cell) and the random initial velocities measured at the center of each cell. Marker particle visualization and velocity visualization are toggled by pressing the 'm' and 'v' keys. Remember that the velocities are actually stored as vectors perpendicular to the face of each cell, visualized by red (x) and green (y) triangles (toggled by pressing the 'e' key). The velocity at the center of each cell (drawn as a line segment colored red->white) is computed by averaging the velocities at the faces on either side of the cell.

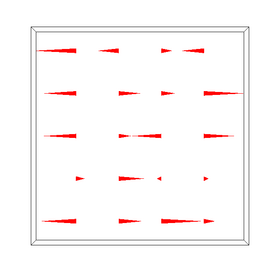
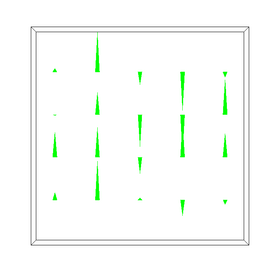
To move particles within the field, we need to compute the velocity at an arbitrary position within the volume (not just the cell center). The simplest (but incorrect) thing to do is just use the velocity at the center of the cell for all particles in that cell. The image below left shows this discontinuous velocity field (press 'd' to visualize this "dense" velocity field). Go ahead and press 'a' to animate the particles within this field and you should see why this isn't a good assignment of velocities.

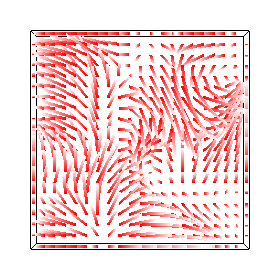
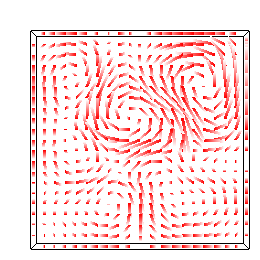
So, your first task is to implement proper velocity interpolation as described in Foster & Metaxas. The interpolation is somewhat complicated because the velocities are defined at the center of each cell face. Study this image from their paper:
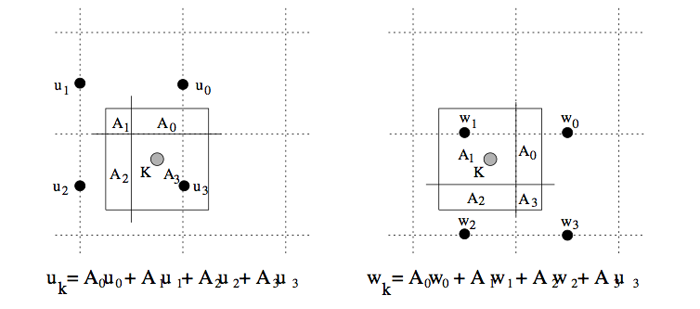
To compute the horizontal component of the velocity at the grey point, k, we determine the indices for the 4 closest u velocities. The horizontal component will be a weighted average of these 4 values. The weights correspond to the 4 subareas in the diagram, formed by cutting a unit square centered at the grey point with unit squares centered at the velocity samples. Intuititively, velocity samples closer to the grey point will have larger area and higher weight. The sum of the areas (& weights) is 1. To find the vertical component of the velocity at the same point, we determine the 4 closest v velocities. Note that the indices (cells) of these points are generally not the same because the u and w velocities are defined on the cell faces so the grids are shifted. Similarly, the areas (weights) are not the same.
Once you've carefully implemented the interpolation in the xy plane, run the above simulation again and you should see dense velocity fields like the ones above middle and right.
NOTE: In the implementation provided, each cell stores the face velocities (u, v, & w) for the face it shares with the cell in the positive direction along each axis. That is, celli,j,k stores ui+1/2,j,k, vi,j+1/2,k, and wi,j,k+1/2. These values are stored in the variables u_plus, v_plus, and w_plus, and the corresponding accessors get_u_plus(), get_v_plus(), and get_w_plus().
-
To perform 3D fluid simulations your interpolation scheme must correctly account for the z direction as well. Of course this is more work! Instead of find the 4 closest velocities for each dimension, you must find the 8 closest values and instead of computing 4 subareas of a unit square, you will compute 8 subvolumes of the unit cube. And you need to do this for each dimension separately. Here are 3 test cases to help you verify that your interpolation is working in 3D. The resulting animation should be symmetric and similar in each of the 3 axis-aligned planes. NOTE: The xy plane is the most important. Even if your z dimension implementation is incomplete or buggy, you can continue with the remainder of the assignment.
./simulation -fluid ../src/fluid_spiral_xy.txt -timestep 0.01 ./simulation -fluid ../src/fluid_spiral_yz.txt -timestep 0.01 ./simulation -fluid ../src/fluid_spiral_zx.txt -timestep 0.01
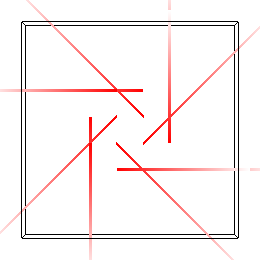
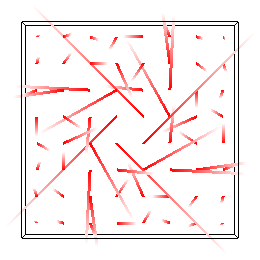
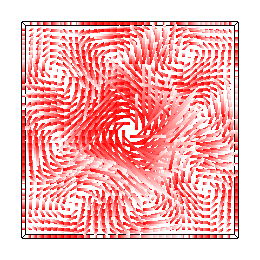
-
Now let's address the issue of compressibility/incompressibility. You may have noticed that your simulations are a little "bouncy". To emphasize the fact, try this simulation:
./simulation -fluid ../src/fluid_compressible.txt -timestep 0.01
You can press "p" to visualize the pressure in each cell by drawing little cubes for each cell colored by pressure. Initially all the cells are white (pressure == 0). After just a few timesteps (press the spacebar to advance by a single timestep) a negative pressure (blue) appears in the middle of the grid surrounded by a ring of positive pressure (red). Later in the simulation these values are quite chaotic, introducing noise into the velocity field.



In order to enforce the incompressibility of the flow, you will need to implement the divergence correction originally described by Harlow & Welch and later by Foster & Metaxas. Compute the divergence of each "full" cell and adjust each non-boundary face velocity to absorb its share of excess inflow or outflow. When correctly implemented, the pressure in each cell should be (within epsilon of) zero throughout the simulation and the flow should no longer "bounce".
./simulation -fluid ../src/fluid_incompressible.txt -timestep 0.01
-
Up to this point, all of the cells in our fluid simulation have been full (had at least one particle). Now let's look at some interesting cases showing the interaction between air and water. Try the examples below. Press "c" to visualize the Marker-And-Cell (MAC) voxels: red == FULL and blue == SURFACE. Press "s" to enable a triangular mesh rendering of the surface using Marching Cubes/Marching Tetras.
./simulation -fluid ../src/fluid_drop.txt -timestep 0.001
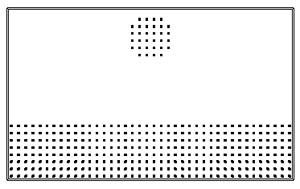
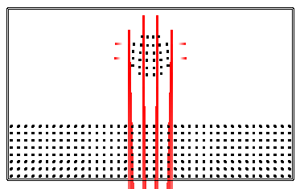
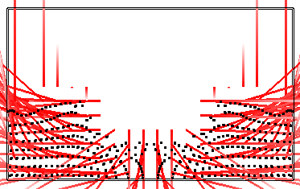


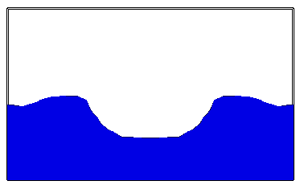
./simulation -fluid ../src/fluid_dam.txt -timestep 0.005

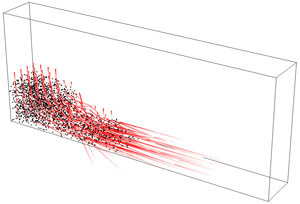
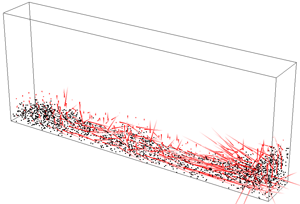
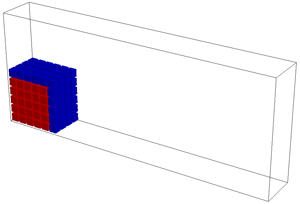
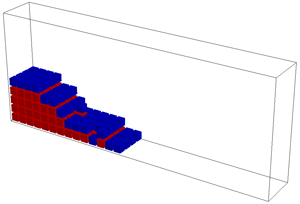

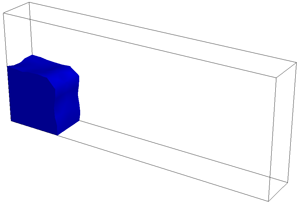
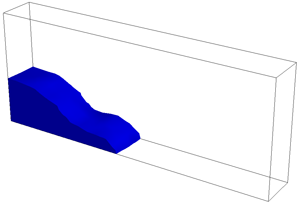
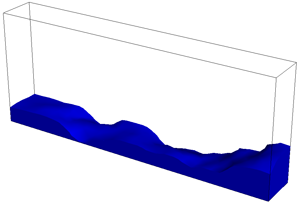
To perform these simulations you will need to extend your incompressibility code to handle surface cells. The divergence of inflow or outflow should be dissipated over the "free" faces of the cell (i.e., faces that this cell shares with EMPTY cells). Note: You can edit the dimensions of your grid by editing the top line of the simulation data file. The "drop" and "dam" shapes will adjust to your new dimensions.
Additional References
-
Practical animation of liquids, Foster & Fedkiw, SIGGRAPH 2001
-
Visual simulation of smoke, Fedkiw, Stam & Jensen, SIGGRAPH 2001
Ideas for Extra Credit
Include a short paragraph in your README.txt file describing your extensions.
-
Implement an alternate integration method (Midpoint, Runge-Kutta, implicit Euler, etc.) for the cloth simulation. Compare the performance of each method.
-
Implement a new visualization/rendering mode (maybe you already did to debug an earlier step). For example, add gouraud shading to the cloth simulation, or use transparency or reflection to improve the water visualization.
-
Create a new cloth or fluid test scene (you can create it procedurally, or create a new input file). A fun fluid test scene could include source and sink cells where mass is created and deleted or a spatial- or time-varying force field (instead of a uniform gravity).
-
Having two physical simulation engines within the same program makes it possible for us to experiment with coupled simulations. Compose a cloth simulation and fluid simulation in the same scene (just load 2 files on the command line). The cloth motion can be driven by the fluid's velocity field, or the fluid motion can be driven by the cloth, or both!
Provided Files (version 2)
Note: Small tweaks not yet tested on Ubuntu & Windows. Please email instructor if you hit out-of-the-box compilation or runtime errors.
-
Basic Code (argparser.h, camera.h, camera.cpp, glCanvas.h, glCanvas.cpp, main.cpp, boundingbox.h, boundingbox.cpp, utils.h, CMakeLists.txt)
Similar to Assignments 0 & 1. Cloth (cloth.h, cloth.cpp)
A class to store, animate, and paint a 2D grid of masses & springs.Cloth test scenes (small_cloth.txt, provot_original.txt, provot_correct_structural.txt, provot_correct_structural_and_shear.txt, denim_curtain.txt, silk_curtain.txt, table_cloth.txt)
Fluid (fluid.h, fluid.cpp, cell.h, marching_cubes.h, marching_cubes.cpp)
Code to store, animate, and render a grid based fluid simulation.Fluid test scenes (fluid_random_xy.txt, fluid_spiral_xy.txt, fluid_spiral_yz.txt, fluid_spiral_zx.txt, fluid_compressible.txt, fluid_drop.txt, fluid_dam.txt)
Files for submission (README.txt and hw2_gradesheet.txt)
Please use the README.txt template for comments about your final submission. Also, to streamline grading, please indicate which portions of the assignment are finished & bug free (full credit), attempted (part credit) or not started (no credit) by filling in the provided hw2_gradesheet.txt and submitting it with your assignment. The grader will then check, edit as needed, and finalize your assessment.
Please read the Homework information page again before submitting.