Query Processing - Sorting and Join#

External Sorting#

A large number of operators can be executed by an intermediate sorting step:
- DISTINCT
- ORDER BY
- GROUP BY
- UNION/INTERSECTION/DIFFERENCE
A limited amount of memory is available to the sort operation

M: the number of memory pages available for the sort operation

PAGES®: total number of disk pages for relation R
If PAGES(R ) <= M, then the relation can be sorted in one pass: read the relation into memory and apply any sorting algorithm. The cost if PAGES(R ) pages.

Multi-step external sorting#

If PAGES(R ) > M, then external sorting must be used.

The sort operation is a two step process:
- STEP 1: Sort groups of M blocks in memory and write each block to disk
- STEP 2: Merge the groups in successive steps into a single sorted relation

Step 1:

for all pages in relation R:
   read data pages for R into M pages
   sor the M pages in memory
   dump the sorted file into a temporary storage

Cost of Step 1:
- Read the relation once and write it once (in groups of M)
  
  Total cost: 2*PAGES(R )

Step 2 (may need to be repeated multiple times):

Merging M sorted groups into one

   Read the first block of each sorted group into a single memory
   buffer (M total)

   Merge by removing the lowest value from all M pages and put in
   the output buffer.

   If a page becomes empty, read the next block for that page
   from disk.

   When all groups are empty, the process is complete.

Note that if there are more than M groups to merge, then we cannot complete the sorting in one merge step. In this case, we need to write the data on disk.

In this case, use M-1 blocks for merging and 1 block for output.

Example for external sort#

Suppose R has 6 pages and we only have M=2 for sorting.

In Step 1, we will read 2 pages of R at a time, sort and then write back to disk:

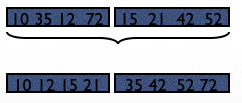
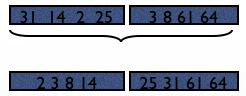
Total cost of step 1: 2*6=12 pages.
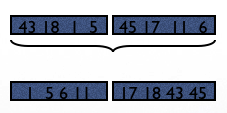
Step 2: Now assume M=3.

Read one page from each group, continuously delete the smallest value and put it in the output buffer.

Given we can read one page from each sorted group, we can finish the sorting in one execution of Step 2.
Total cost of step 2: 1*6 = 6
Overall cost (steps 1 and 2): 12+6 = 18

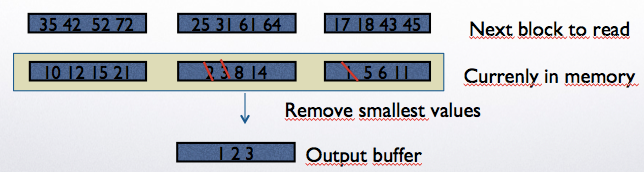
Multi-step version of Step 2#

Let us see a different example.

Suppose PAGES(R )=1,000 and M = 11
Step 1: We create 91 sorted groups (total cost 2,000 pages)
In Step 2, we cannot really merge all 91 groups (since M=11). We have to sort and write groups.

We can merge 10 groups (and use 1 block for output) at a time.

Reduce: 91 sorted groups to 10 sorted groups

Total cost: 2,000 pages (read once, write once)
We can repeat Step 2 to merge the remaining 10 groups and output the result.

Total cost: 1,000 pages (read once and output)
Total cost: 5,000 pages.
For simplicity, we can just disregard the 1 output buffer in our computations.

Nested loop join#

The naïve approach R join S (R outer, S inner)

For each one page of the outer relation (R):
     read the page into 1 block of memory
     for all pages of the inner relation (S):
         read the page into 1 block of memory
         join with the block in memory

Needs only 2 blocks of memory
For each block of R, S is read once.

S is read a total of PAGES(R ) times, total blocks of S read is then PAGES(R )*PAGES(S)

R is read once, therefore the total cost is PAGES(R )+PAGES(R )*PAGES(S)

Block nested loop join#

Given M buffer pages for the query

for each M-1 block chunks of outer relation(R)
   read M-1 pages R into memory
   for each page of inner relation (S)
       read the page into 1 memory block
           join the tuples in S with all pagse of R in memory

S is read a total of ceiling(PAGES(R )/(M-1)) times, total I/O cost of S is then PAGES (S)* ceiling(PAGES(R )/(M-1))
As always, R is read once. So, the total cost is

PAGES(R ) + PAGES(S)* ceiling(PAGES(R )/(M-1))

Index nested loop join#

Index loop join assumes a look-up of matching tuples for S using an index.

Given R join S on R.A=S.A

Read R one block at a time
   For each tuples r of R
      Use index on S(A) to find all matching tuples
      Read the tuples from disk and join with

If R is not sorted on A, then we might end up reading the same tuples of S many times
- What if A is R’s primary key?
  
  Then, for each A value, we will look up S only once
Cost:
- The outer relation R is read once, PAGES(R )
- Assume for every tuple r in R, there are about c tuples in S that would join with R (ideal case is c is very small or 0 most of the time)
- Then, for each tuples in R: - We find the matching tuples in S (cost is index look-up, in the
  
  best case one tuple for each level, so h+1 for an index with h levels)
  - Then, if we need attributes that are not in the join, we read c tuples from S (which can be in c pages in the worst case)
  - Total cost is between PAGES(R ) + TUPLES® * (h+1) (if no tuples match or index only scan is fine) and PAGES(R ) + TUPLES® * (h+1+c)

Example:

SELECT S.B FROM R,S WHERE R.A = S.B

Index I1 on S(B) with 2 levels (root, internal, leaf)
PAGES(R )=100, TUPLES(R)= 2000
PAGES(S)=200, TUPLES(S)= 4000

Cost = 100 (for reading R) + 2000*3 (index look up for each tuple of R)

SELECT S.C  FROM R,S WHERE R.A = S.B

Assume statistics are same as above, but we now need to reach
each matching tuple (at most 4000 tuples will match)

Cost = 100+2000*3+4000 (one page read for each matched tuple)

How could this be, there are only 200 pages of S?

Well, if we are not finding all pages that we need to read first and reading each page as we find a match, we may end up reading the pages for S multiple times.

Of course, in reality, you will likely do a lot of reduction of duplicate page requests in memory and improve on this. This is the worst case scenario.

Will we ever do this?

No, we will choose not to use index join for this case, clearly it looks very expensive and we better do some other operation.

Another example:

SELECT S.B FROM R,S WHERE R.A = S.B AND R.B=100

Index I1 on S(B) with 2 levels (root, internal, leaf)
PAGES(R )=100, TUPLES(R)= 2000
PAGES(S)=200, TUPLES(S)= 4000
Suppose only 3 tuples match R.B=100

So, we can:
   Scan all of R to find these 3 tuples (100 pages)
   Read matching tuples from S (3*3)
   Total cost = 109 (using only 2 pages of memory)

   This would cost a lot more in block-nested loop join
   with M=2 (200 pages). So, index join is for cases
   where the outer relation is very small (normally after
   a selection)

Query Processing - Sorting and Join

Contents