Lecture 22#
Lecture exercise out today, due on saturday at midnight
Hope to release another optional lecture exercise, timing is unknown
Hope to release Hw#6 before the week ends
Exam#2 grading to be completed very soon (though probably not today)
Hw#5 grading is next
B-tree indices and index scan#
Review of search/insertion/deletion
Handling indices with multiple attributes
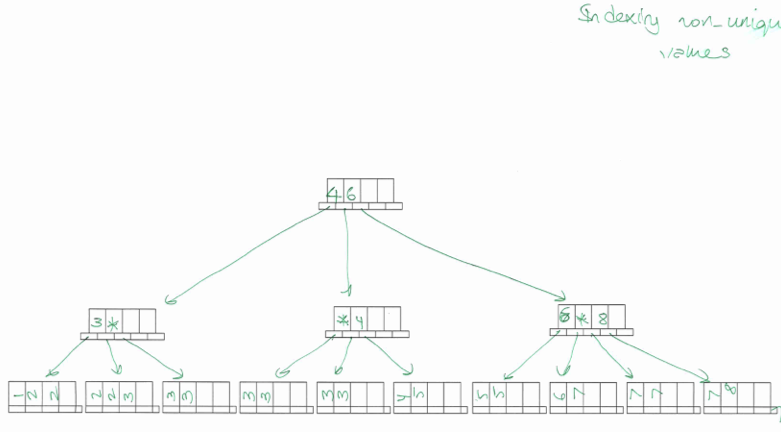
Handling indices with duplicate key values
Index search for answering select queries
Generalizing B-tree indices
Suppose we have the following query:
SELECT A,B,C,D FROM R WHERE R.A=10 AND R.B>5 AND R.B<10 AND R.C > 20;
And indices:
I1 on R(A)
I2 on R(B)
I3 on R(B,A,C)
I4 on R(A,B,C,D)
Possible access paths:
Sequential scan: read all pages of R
Use index I1:
find all tuples with A=10,
read the matching tuples from disk and check on B and C conditions,
output A,B,C,D
Use index I2:
find all tuples with B<10,
read the matching tuples from disk and check on A and C conditions,
output A,B,C,D
Use index I1, find all tuples with A=10
Use index I2, find all tuples with B<10,
Find the intersection of tuples to find those that satisfy both
read the matching tuples from disk and check on C condition,
output A,B,C,D
Use index I3, on R(B,A,C) :
Start the search at A=10 and B>5, end the scan at B>=10 (more or less same as the search for B>5 and B<10).
Find all tuples that satisfy conditions on A,B and C
Read the tuples to returnt the missing D value
Use index I4 on R(A,B,C,D)
Scan the index for A and B conditions
Return the A,B,C,D values of the found tuples that satisfy A,B,C conditions
This is called an index only scan
Assume a page has 8000 bytes of addressable space, a tuple pointer is 10 bytes
movieroles(actorid, movieid, role, info1, info2)
TUPLES(movieroles) = 265K PAGES(movieroles) = 2048
`select actorid, role from movieroles where actorid = 123;’
Cost = 2048
Index I1 on mr(actorid)
4+10= 14 bytes per entry
Index can store 570 entries per page. (8000/14)
Leaf level has 465 nodes (if all nodes are 100% full) – the tree will have 2 levels (root and leaf)
Leaf level has 665 nodes (if all nodes are 70% full) – the tree will have 3 levels (root, internal, leaf)
Index I2 on mr(movieid)
Same as I1
Index I3 on mr(movieid, actorid)
4+4+10= 18 bytes per entry
Index can store 445 entries per page. (8000/18)
Leaf level has 851 nodes (if all nodes are 70% full) – the tree will have 3 levels (root, internal, leaf)
Index I4 on mr(actorid, movieid, role)
4+4+15+10=23 bytes per entry
Index can store 347 entries per page
1091 leaf nodes at 70% full – the tree will have 3 levels (root, internal, leaf)
Assume indices are 70% full:
`select movieid, role from movieroles where actorid = 1234;’
Sequential scan: Cost = 2048
Index I1, (assume about 5 movies per actor), 1 or 2 leaf nodes to scan
Index scan: 1 root, 1 internal, 1 or 2 (worst case) leaf nodes = 4 disk pages
Read the matching 5 tuples from disk (worst case 5 different pages)
Total cost = 4 (index scan) + 5 (reading the tuples) = 9 pages
I2 not usable for this query
I3:
Index scan:Scan root, internal and then all leaf: 2+ 851 nodes
Read the matching 5 tuples from disk for the “role” attribute (worst case 5 different pages)
Total cost: 853+5= 858
I4:
Index scan: 1 root, 1 internal, 1 or 2 (worst case) leaf nodes = 4 disk pages
Return movieid, role directly from the index
Total cost = 4 (index scan) = 4 pages
1091/(347*.70)
4.491560312885961