Lecture 25 - Query Optimization and Concurrency in Transactions

Lecture 25 - Query Optimization and Concurrency in Transactions#

Today’s topics:#

  • Query Optimization

  • Concurrency:

    • Definition of serial and serializable schedules

    • Checking of serializable schedules

    • 2 Phase Locking

Announcements#

  • Office hours

    • My office hours today are from 2:15-3:15PM

    • I will hold office hours next week as usual: 2:30PM-5PM

    • Any additional office hours will be posted on Bulletin Board

    • Please ask questions on Bulletin board

  • Remaining lectures:

    • Today: Query Optimization and Concurrency in Transactions

    • Thursday: Concurrency in Transactions continued and Database Tuning

  • Remaining assignments:

    • Hw6: Due on today midnight

    • Lecture Exercise 24: due on Friday 12/12

    • Optional Lecture Exercise 3: due on Friday 12/12

    • Lecture Exercise 25: out today, due on Friday 12/12

  • We will drop the lowest 5 lecture exercises (despite the weird naming convention I used!). So two of these exercises can be treated as optional.

  • Use lecture exercises to study! Just because we drop some does not mean the material in them is optional. They are there for you to study.

  • Final Exam is on 12/18, 11:30AM-2:30PM on DCC 308

    • If you need extra time, expect to take the exam between 11:30AM-4PM

    • Notify me of any conflicts if you have not done so

Query optimization#

  • Parse the query and simplify conditions if possible

  • Consider different query trees

    • Join ordering

      • ( R join S vs S join R),

      • (R join S) join T vs (R join T) join S

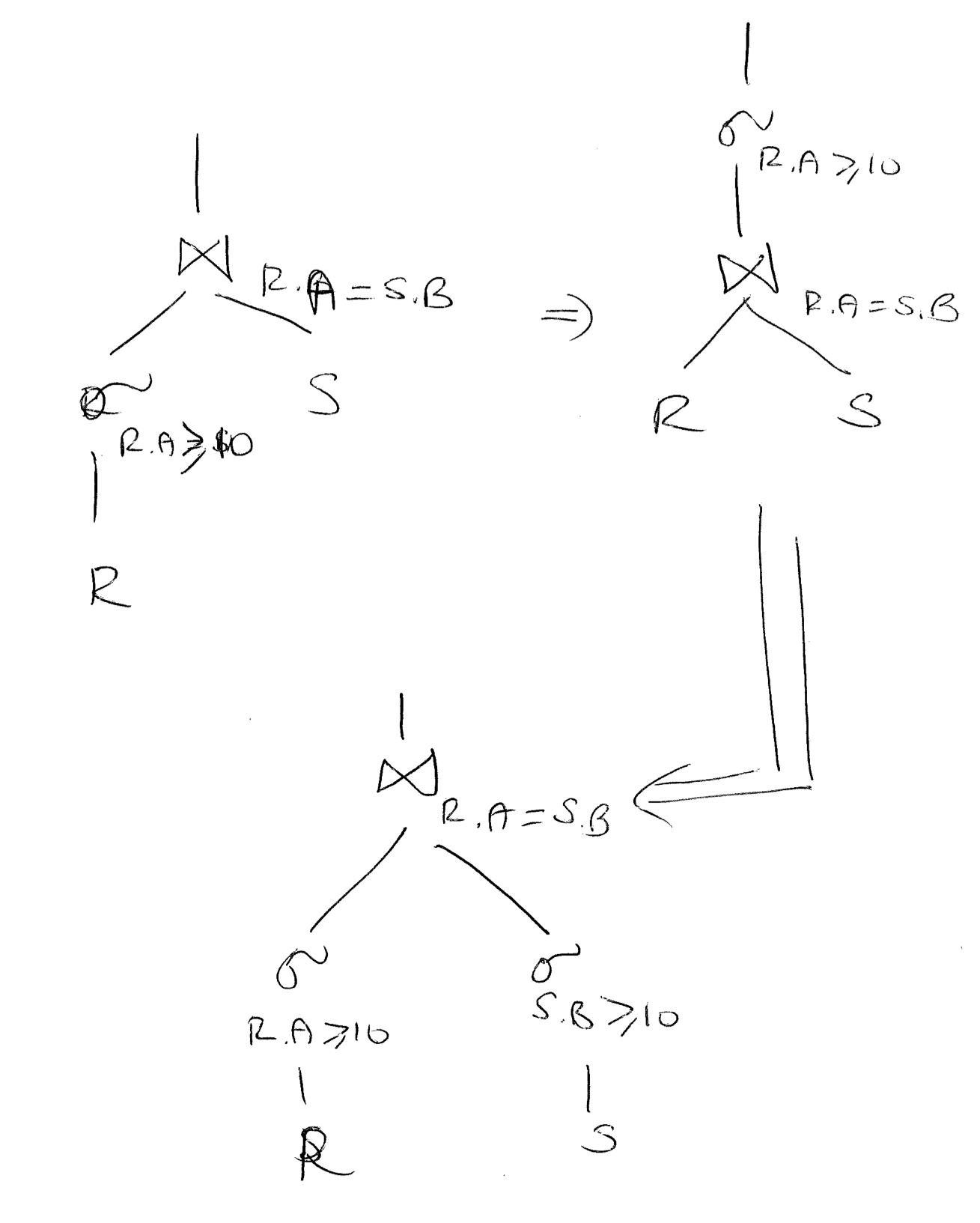
    • Consider pushing selections down joins

      • Potentially reduce size/cost of joins and allow for index scans

      • select_C (R join S) = select_C® join select_C(S)

    • Sorting may be beneficial (so consider sorting even if in the intermediate steps it appears too costly)

  • Query optimization works as a search algorithm:

    • Consider all possible 2- way joins (and selections/sorts applicable)

    • Add a third relation, and eliminate any 2-way joins that are too costly (compared to a 3-way join)

    • Continue until the whole query is implemented

Query Optimization 1 Join Ordering Pushing Selections Down

Transactions (xact) - Concurrency - Isolation#

  • A transaction has an beginning and an end point

BEGIN TRANSACTION ;
select ...
insert ...
delete ...
COMMIT ;

  • Atomicity of transactions:

    • Either all the transaction succeeds and all the changes it made are final, or the transaction has no effect in the database.

    • This includes all the impacts of the transaction that becomes a part of the transaction: e.g. foreign key cascade/set null, triggers.

  • Isolation of transactions:

    • We write xacts assuming it is the only one executing or even if other xacts are executing, it will not cause a problem.

  • There is no problem if only one transaction executes in the database.

    • So if the xacts executed serially!, then the result would be fine.

  • A parallel execution of xacts if also fine! (no problem), if the result is the same as one of a serial order of xacts.

    • This is called a serializable execution.

Let us see two different transactions and the result of their potential serial executions.

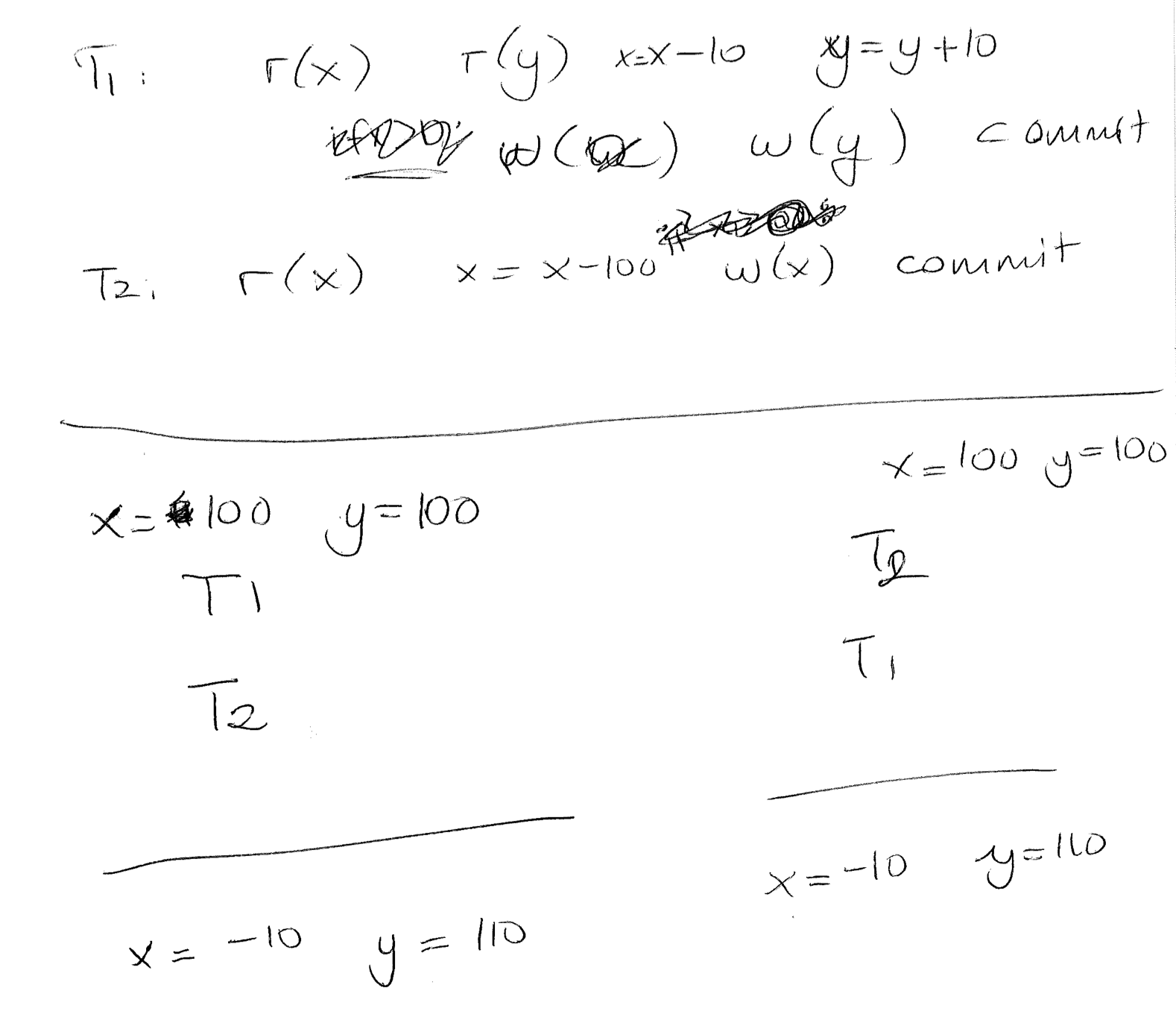
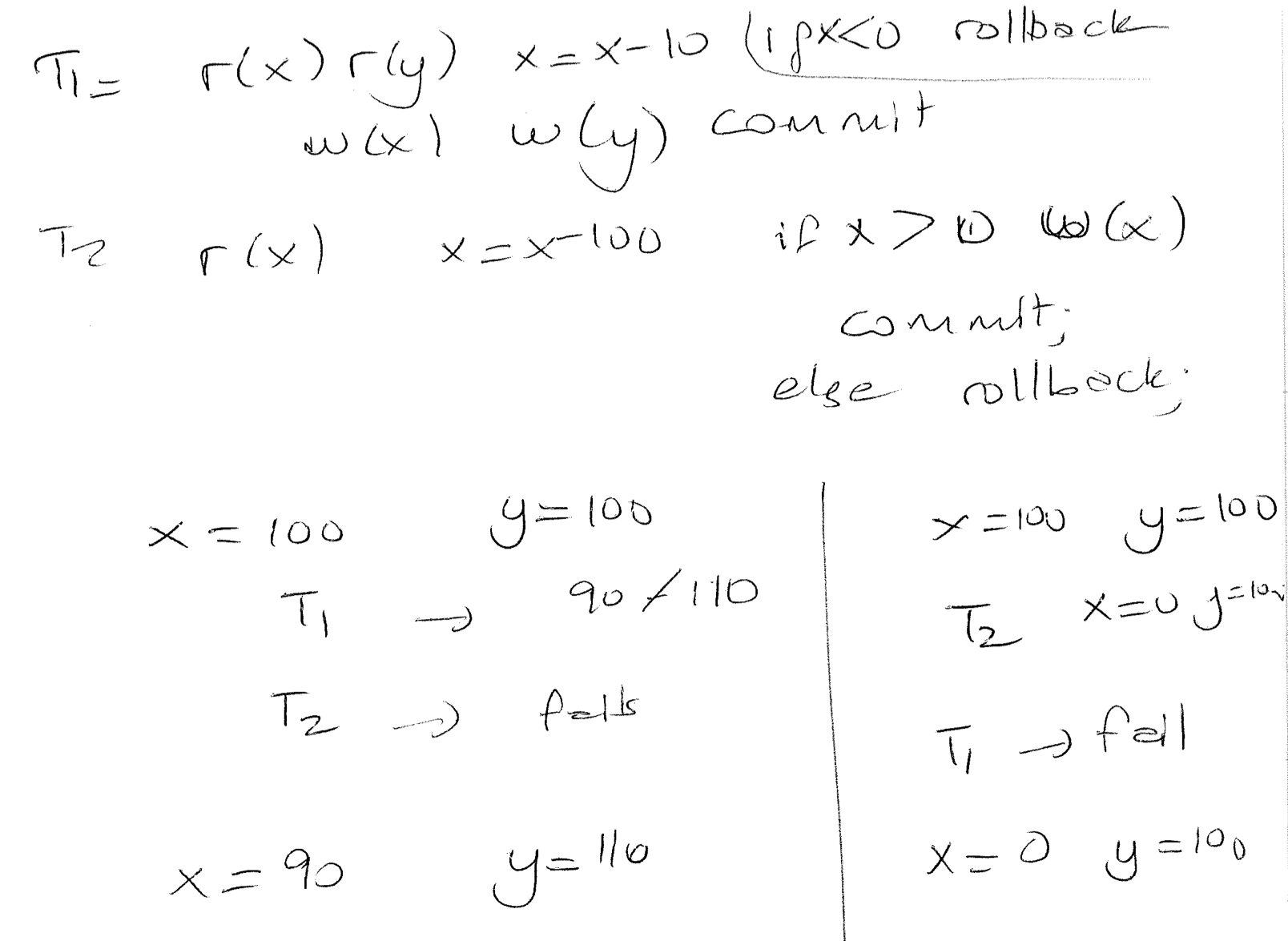
Transaction model 1 Transaction model 2

Now let us see a different execution which does not produce the same results as any serial execution.

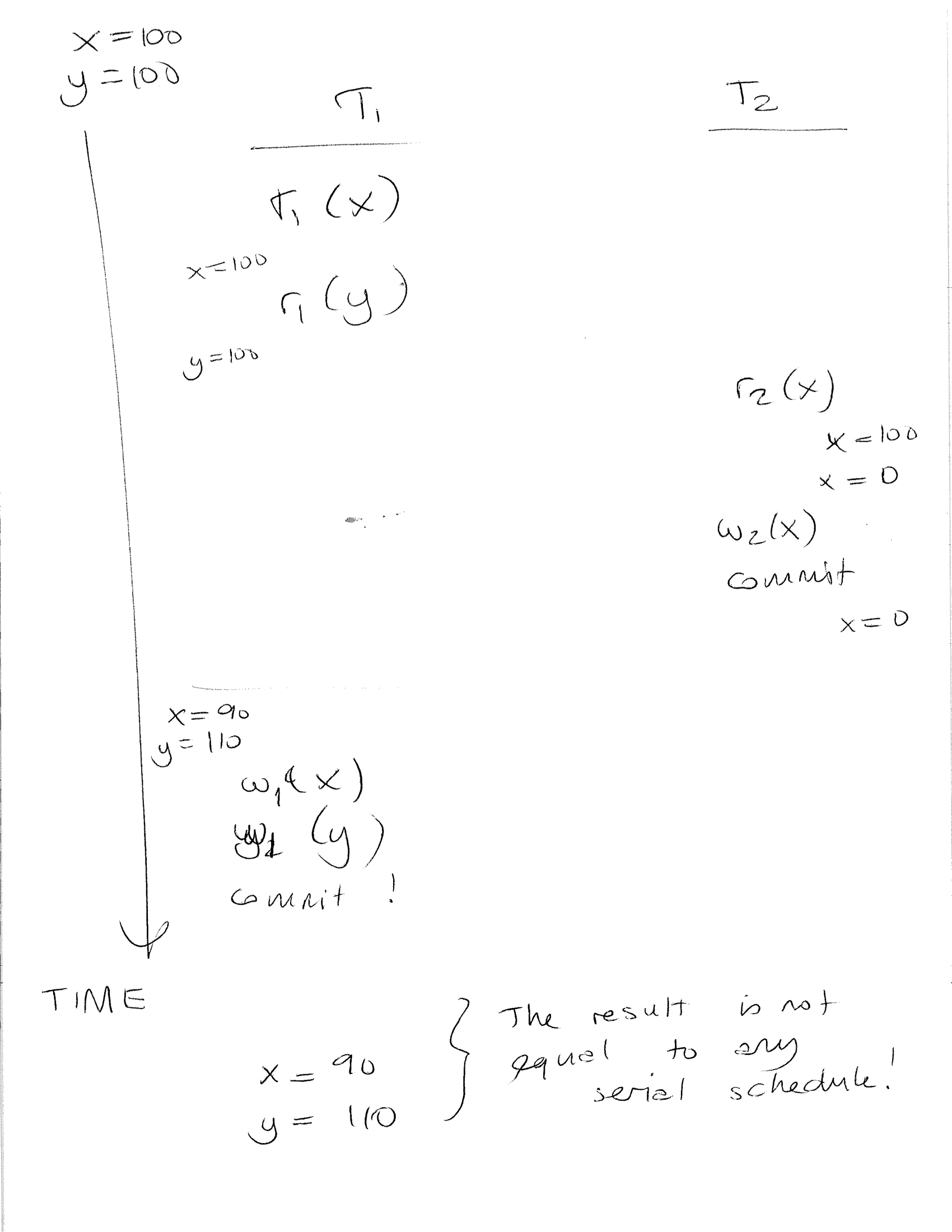
Transaction model 1

Serializable Transactions

  • Simplify transactions into read/write operations

    • T1: r1(x) r1(y) w1(x) w1(y) c

    • T2: r2(x) w2(x) c

  • Simplify the execution of operations into schedules (ordering of the transaction operations):

    • s1: r1(x) r1(y) w1(x) w1(y) r2(x) w2(x)

    • s2: r2(x) w2(x) r1(x) r1(y) w1(x) w1(y)

    • s3: r1(x) r1(y) r2(x) w2(x) w1(x) w1(y)

    • s4: r1(x) r1(y) w1(x) r2(x) w1(y) w2(x)

  • A schedule is serializable if there exists a serial order of transactions S such that all reads are guaranteed to have the same value as serial order S and if all writes occur in the same order as the serial order S.

  • A conflict in a schedule is two operations by two different transactions on the same item and one of them is a write operation.

  • Conflicts:

    • r1(x) … w2(x)

    • w1(x) … r2(x)

    • w1(x) … w2(x)

  • If the ordering of a conflicting operation is changed, the final result of the transaction may change.

    • r1(x) … w2(x) vs… w2(x) … r1(x)

    • w1(x) … w2(x) vs. w2(x) … w1(x)

  • A schedule is serializable if there exists a serial order of transactions S such that all conflicting operations in the schedule occur in the same order as a serial schedule.

    • s1: r1(x) r1(y) w1(x) w1(y) r2(x) w2(x)

    • s2: r2(x) w2(x) r1(x) r1(y) w1(x) w1(y)

  • Given s4: r1(x) r1(y) w1(x) r2(x) w1(y) w2(x) list all conflicts:

r1(x) w2(x) w1(x) r2(x) w1(x) w2(x)

  • Given s1: r1(x) r1(y) w1(x) w1(y) r2(x) w2(x) list all conflicts:

r1(x) w2(x) w1(x) r2(x) w1(x) w2(x)

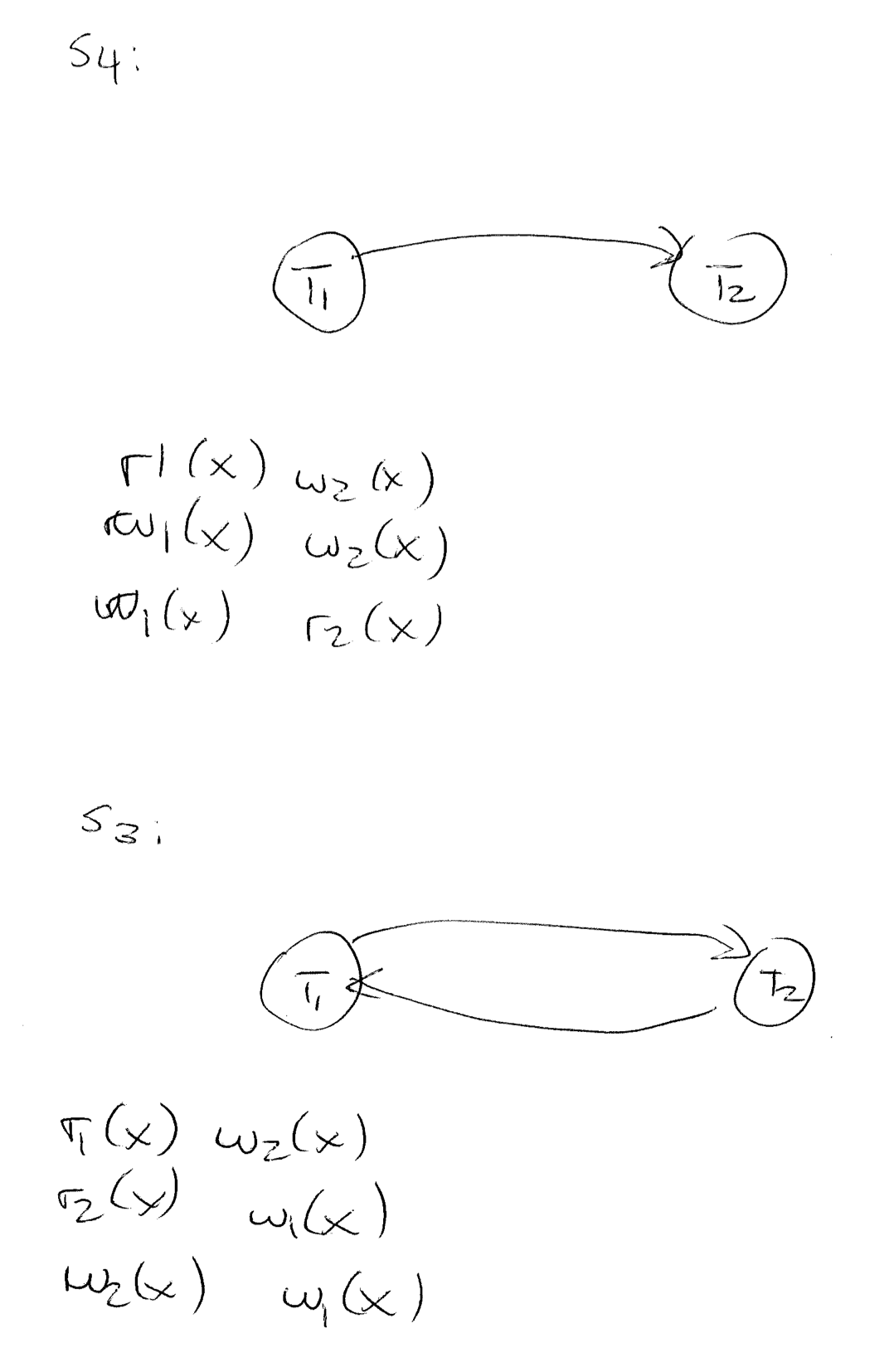
  • All conflicts in s4 occur in the same order as s1. s1 is a serial schedule (T1 T2). Hence, s4 is serializable.

  • Given s3: r1(x) r1(y) r2(x) w2(x) w1(x) w1(y) list all conflicts:

r1(x) w2(x) r2(x) w1(x) w2(x) w1(x)

  • There is no serial order that has this ordering!

    • T1 T2 (r2(x) w1(x), w2(x) w1(x) not possible)

    • T2 T1 (r1(x) w2(x) not possible)

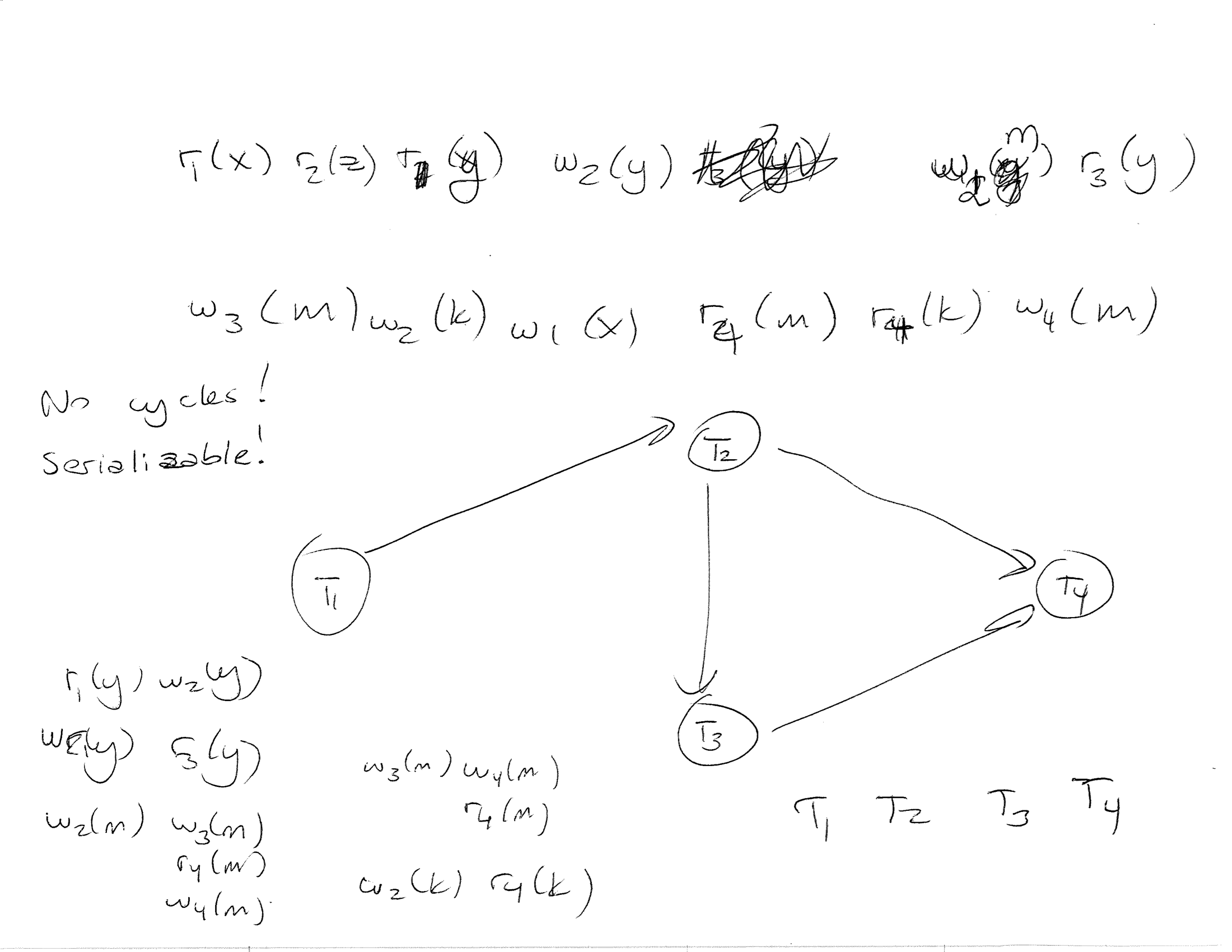
Conflict Graph

  • Each transaction is a node

  • For every conflict T1…T2 (such as r1(x) w2(x) or w1(x) w2(x)), there is an edge from T1 to T2

  • If the graph has a cycle, then the given schedule is not serializable

  • If the graph has no cycles, then the given schedule is serializable and we can find the corresponding serial schedule using topological search on the conflict graph

Conflict Graph Conflict Graph

Contents