Homework 0: Transformations & OpenGL Warmup

The goal of this warmup assignment is to get comfortable with the programming environment you will be using for this class and familiarize yourself with a simple library that we will use for linear algebra. It's also an opportunity for a crash course in C++ and OpenGL (if you're not already familiar with them). This assignment is only worth 1/4 of the points of a regular homework assignment. It will not be rigorously graded, but you are expected to work through and submit the exercises. Please try to finish this assignment by the end of the first week of classes; however, there is no firm deadline for this assignment.

Here are a couple tutorials you may want to check out:

• C++ Tutorial

• Linear Algebra Review

The incidental goal is also to have fun with bizarre fractal objects. IFS are self-similar fractals: a subpart of the object is similar to the whole. The classic example of an IFS is Barnsley's fern, where each subpart of the fern is exactly the same as the whole fern. IFS are described by a set of affine transformations (rotations, translations, scale, skew, etc.) These transformations capture the self-similarity of the object. IFS can be defined in any dimension, and we will play with both two-dimensional and three-dimensional ones. Formally, an IFS is defined by n affine transformations. Each transformation f_i must be contractive: The distance between points must be reduced. An attractor of the IFS is the object such that A = U f_i (A). A is unchanged by the set of transformations: It is a fixed point.

We can render an IFS by iterating the transform on random input points from the unit square. We approximate the fixed point by applying the transformation many times. The algorithm is as follows:

   for "lots" of random points (x0, y0)
       for k=0 to num_iters 
           pick a random transform fi
           (xk+1, yk+1) = fi(xk, yk)
       display a dot at (xk, yk)

To minimize the number of points necessary to make an image of reasonable quality, probabilities are assigned to each transformation, instead of choosing a transformation with uniform probability.

Tasks

• Download the provided source code and set up your C++ development environment. To receive full credit, your homework assignments must compile and run without errors using our build instructions on Linux, Mac OSX, or Windows. Please follow these instructions closely for installation on your system and compiling the code:

  • Graphics Library Installation Notes

  • Notes on Using CMake

  A CMakeLists.txt file is provided and has been tested on Linux(gcc), MacOSX(llvm/clang), and Windows(Visual Studio). Please see the TA or instructor in office hours if you have trouble setting up your development environment.

• The initial executable from the provided code should launch an OpenGL window and draw a cube of noisy points or a solid cube. Try these commands:

     ./ifs -input ../src/sierpinski_triangle.txt 
     ./ifs -input ../src/sierpinski_triangle.txt -cubes
  

  Note: You need to specify an input file (even though that data is ignored in the provided code) so that the program can find the fragment & vertex shaders (which are assumed to be in the same directory as the input file).

  You should be able to navigate the scene with the mouse: left button rotates, middle button -or- control+mouse translates, and shift+mouse zooms.

• Now you're ready to start coding. Study the IFS class and extend it to store the transformations & probabilities from the input file.

• Edit the drawing code to use the GLM -- OpenGL Mathematics Library to transform the points and create and render multiple cubes to visualize the IFS.

• Consider the performance of your programming environment. How many polygons/points can you render interactively? What improvements could you make to your code? Discuss in your README.

Possible Extensions

Extra credit is available for creative extensions. Examples include:

• design a new IFS --- figure out the transformations and probabilities,

• implement an interesting, non trivial color scheme,

• implement anti-aliasing,

• experiment with depth-first vs. breadth-first, etc.

Include a short paragraph in your README.txt file describing your extension(s).

Hints

• To debug your code, set the number of iterations to one. This will allow you to check that you got the transformations right.

• Be careful, arrays are indexed from 0 to n-1 in C++. Reading beyond the bounds of the array will probably result in a segmentation fault.

• Use assert() to check function pre-conditions, array indices, etc.

Provided Files: provided_files.zip

NOTE: If you are using GLUT instead of GLFW/GLEW/GLM, see last year's page & last year's code.

• Parsing code for command-line arguments and input files (argparser.h)
  The program takes a number of command line arguments to specify the input file (-input), number of points (-points), number of iterations (-iters), and window height & width (-size). Your program should render points by default, or cubes if -cubes is specified. Examples are shown below. Code to parse input files and command line arguments is provided.

• OpenGL and main code (main.cpp, ifs.h, ifs.cpp, glCanvas.h, glCanvas.cpp, camera.h, camera.cpp)
  OpenGL programs can be tricky to set up from scratch. This base code should do all that work for you.

• Random Number Generator (MersenneTwister.h)
  A great tool for high quality random numbers from
  http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html

• Simple Shaders (ifs.vertexshader and ifs.fragmentshader)
  

• Data files (fern.txt, dragon.txt, sierpinski_triangle.txt, and giant_x.txt)
  The input data for an IFS is a file which contains n, the number of transforms, followed by the probability of choosing each transform and a 4x4 floating point matrix representation of the transform.

• Files for compilation (CMakeLists.txt, FindGLFW.cmake, and FindGLM.cmake)
  Follow the Graphics library installation & CMake compilation instructions for your operating system.

• Files for submission (README.txt and hw0_gradesheet.txt)
  Fill out these files before submitting your assignment.

Sample Results

./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 0 -size 200
./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 1 -size 200
./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 2 -size 200
./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 3 -size 200
./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 4 -size 200
./ifs -input ../src/sierpinski_triangle.txt -points 10000 -iters 30 -size 200

./ifs -input ../src/fern.txt -points 50000 -iters 30 -size 400

./ifs -input ../src/giant_x.txt -points 10000 -size 400 -iters 0
./ifs -input ../src/giant_x.txt -points 10000 -size 400 -iters 1
./ifs -input ../src/giant_x.txt -points 10000 -size 400 -iters 2
./ifs -input ../src/giant_x.txt -points 10000 -size 400 -iters 3
./ifs -input ../src/giant_x.txt -points 10000 -size 400 -iters 4

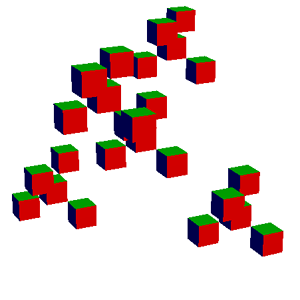
Now here's an example using the -cubes argument. Each cube represents the bounding box of the cloud of random 3D points that are transformed in each iteration. There are a couple different ways to implement this rendering mode.

./ifs -input ../src/giant_x.txt -size 400 -iters 0 -cubes
./ifs -input ../src/giant_x.txt -size 400 -iters 1 -cubes
./ifs -input ../src/giant_x.txt -size 400 -iters 2 -cubes
./ifs -input ../src/giant_x.txt -size 400 -iters 3 -cubes
./ifs -input ../src/giant_x.txt -size 400 -iters 4 -cubes

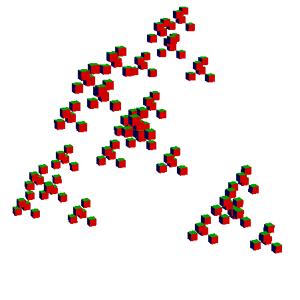
Please read the homework information page again before submitting.